题目内容
命题P:tan(A+B)=0,命题Q:tan A+tan B=0,则P是Q的
- A.充要条件
- B.充分不必要条件
- C.必要不充分条件
- D.既不充分也不必要条件
C
分析:举反例得到P不一定推出Q,证明Q能推出P,得到P是Q的必要不充分条件即可.
解答:由tan(A+B)=0得A+B=kπ,假如k=1,A=B= ,得到tanA+tanB无意义,所以不为充分条件;
,得到tanA+tanB无意义,所以不为充分条件;
而当tan A+tan B=0时,tan(A+B)=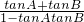 =0,为必要条件.
=0,为必要条件.
所以P是Q的必要不充分条件.
故选C.
点评:考查学生会证明两个命题之间的关系,灵活运用三角函数的恒等变换.证明不成立可采用举反例的方法.
分析:举反例得到P不一定推出Q,证明Q能推出P,得到P是Q的必要不充分条件即可.
解答:由tan(A+B)=0得A+B=kπ,假如k=1,A=B=
 ,得到tanA+tanB无意义,所以不为充分条件;
,得到tanA+tanB无意义,所以不为充分条件;而当tan A+tan B=0时,tan(A+B)=
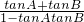 =0,为必要条件.
=0,为必要条件.所以P是Q的必要不充分条件.
故选C.
点评:考查学生会证明两个命题之间的关系,灵活运用三角函数的恒等变换.证明不成立可采用举反例的方法.

练习册系列答案
相关题目
命题P:tan(A+B)=0,命题Q:tan A+tan B=0,则P是Q的( )
| A、充要条件 | B、充分不必要条件 | C、必要不充分条件 | D、既不充分也不必要条件 |