题目内容

∫
π
2
-
π
2
(sinx+cosx)dx的值是
 
．
分析：求出原函数，依定义代入上下限的值，求出即可
解答：解：
∫
π
2
-
π
2
(sinx+cosx)dx=（-cosx+sinx）
|
π
2
-
π
2
═1+1=2
故答案为2
点评：本题考查定积分的定义，求解本题的关键是掌握好定义，并熟练掌握常见的函数的导数．
练习册系列答案
相关题目
已知向量
a
=(
3
，1)，向量
b
=(sinα-m，cosα)．
（Ⅰ）若
a
∥
b
，且α∈[0，2π），将m表示为α的函数，并求m最小值及相应的α值；
（Ⅱ）若
a
⊥
b
，且m=0，求
cos(
π
2
-α)•sin(π+2α)
cos(π-α)
的值．
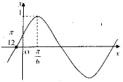精英家教网函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜
π
2
）的一部分图象如图所示，将函数f（x）图象上每一点的纵坐标不变，横坐标伸长为原来的2倍得到图象表示的函数可以为（　　）
A、y=sin（x+
π
6
）
B、y=sin（4x+
π
6
）
C、y=sin（x+
π
12
）
D、y=sin（4x+
π
3
）
已知向量
a
=（-2，sinθ）与
b
=（cosθ，1）互相垂直，其中θ∈（
π
2
，π）．
（1）求sinθ和cosθ的值；
（2）若sin（θ-φ）=
10
10
，
π
2
＜φ＜π，求cosφ的值．
将函数y=sin(2x+
π
4
)的图象向左平移
π
4
个单位，再向上平移2个单位，则所得图象的函数解析式是（　　）
（2013•徐州模拟）[选修4-4：坐标系与参数方程]
在极坐标系中，已知点P为圆ρ2+2ρsinθ-7=0上任一点．求点P到直线ρcosθ+ρsinθ-7=0的距离的最小值与最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网