题目内容
(2013•徐州模拟)[选修4-4:坐标系与参数方程]
在极坐标系中,已知点P为圆ρ2+2ρsinθ-7=0上任一点.求点P到直线ρcosθ+ρsinθ-7=0的距离的最小值与最大值.
在极坐标系中,已知点P为圆ρ2+2ρsinθ-7=0上任一点.求点P到直线ρcosθ+ρsinθ-7=0的距离的最小值与最大值.
分析:由题意圆的普通方程为 x2+y2+2y-7=0,参数方程为
(α为参数),直线的极坐标方程为ρcosθ+ρsinθ-7=0.将圆和直线先化为一般方程坐标,然后再计算椭圆上点到直线距离的最大值和最小值即可.
|
解答:解:圆ρ2+2ρsinθ-7=0的普通方程为 x2+y2+2y-7=0,…(2分)
直线ρcosθ+ρsinθ-7=0的普通方程为x+y-7=0,…(4分)
设点P(2
cosα,2
sinα-1),
则点P到直线x+y-7=0的距离
d=
=
…(8分)
所以dmin=
=2
,
dmax=
=6
.…(10分)
直线ρcosθ+ρsinθ-7=0的普通方程为x+y-7=0,…(4分)
设点P(2
| 2 |
| 2 |
则点P到直线x+y-7=0的距离
d=
|2
| ||||
|
|4sin(α+
| ||
|
所以dmin=
| 4 | ||
|
| 2 |
dmax=
| 12 | ||
|
| 2 |
点评:此题考查参数方程、极坐标方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,这也是每年高考必考的热点问题.

练习册系列答案
相关题目
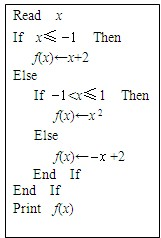 (2013•徐州模拟)已知某算法的伪代码如图,根据伪代码,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是
(2013•徐州模拟)已知某算法的伪代码如图,根据伪代码,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是