题目内容
(本小题满分15分)
设关于x的方程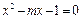 有两个实根
有两个实根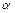 、
、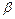 ,且
,且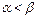 .定义函数
.定义函数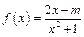 .
.
(Ⅰ)求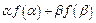 的值;
的值;
(Ⅱ)判断 在区间
在区间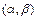 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅲ)若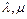 为正实数,证明不等式:
为正实数,证明不等式: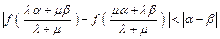 .
.
设关于x的方程
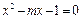 有两个实根
有两个实根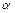 、
、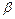 ,且
,且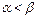 .定义函数
.定义函数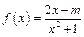 .
.(Ⅰ)求
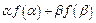 的值;
的值;(Ⅱ)判断
 在区间
在区间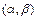 上的单调性,并加以证明;
上的单调性,并加以证明;(Ⅲ)若
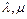 为正实数,证明不等式:
为正实数,证明不等式: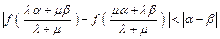 .
.(Ⅰ)
(Ⅱ) 在
在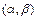 上为增函数,证明略
上为增函数,证明略
(Ⅲ) 证明略
证明略

(Ⅱ)
 在
在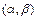 上为增函数,证明略
上为增函数,证明略(Ⅲ)
 证明略
证明略(Ⅰ)解:∵ 是方程
是方程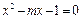 的两个实根
的两个实根
∴
∴
同理
∴ …………5分
…………5分
(Ⅱ)∵
∴ …………8分
…………8分
当 时,
时,
而
∴ 在
在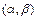 上为增函数 …………10分
上为增函数 …………10分
(Ⅲ)∵ 且
且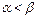
∴

∴ …………12分
…………12分
由(Ⅱ)可知
同理可得
∴
∴ …………14分
…………14分
又由(Ⅰ)知
∴
所以 …………15分
…………15分
 是方程
是方程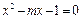 的两个实根
的两个实根∴

∴

同理

∴
 …………5分
…………5分(Ⅱ)∵

∴
 …………8分
…………8分当
 时,
时,
而

∴
 在
在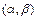 上为增函数 …………10分
上为增函数 …………10分(Ⅲ)∵
 且
且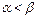
∴


∴
 …………12分
…………12分由(Ⅱ)可知

同理可得

∴

∴
 …………14分
…………14分又由(Ⅰ)知

∴

所以
 …………15分
…………15分
练习册系列答案
相关题目
 的解组成的集合为__________________.
的解组成的集合为__________________. 是同一个函数的是 ( )
是同一个函数的是 ( )



 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度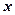 不得
不得 超过
超过 米,房屋正面的造价为400元
米,房屋正面的造价为400元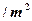 ,房屋侧面的造价为150元
,房屋侧面的造价为150元 表示成
表示成 )=f(x)-f(y).
)=f(x)-f(y). )<2.
)<2.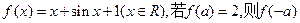 的值为 。
的值为 。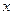

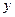
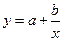
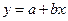
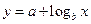
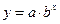
 ②
②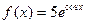 ;③
;③ ;④
;④ 。
。 定义域内的任意一个自变量
定义域内的任意一个自变量 ,都存在唯一的自变量
,都存在唯一的自变量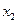 ,使
,使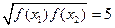 成立的函数为 ( )
成立的函数为 ( ) 对任意实数
对任意实数 都有
都有 ,且
,且 ,则实数
,则实数 的值等于
的值等于