题目内容
9.下列函数中,在(-∞,0)上为减函数的是( )| A. | $y={x^{\frac{2016}{2015}}}$ | B. | $y={x^{\frac{2013}{2015}}}$ | C. | $y={x^{-\frac{2014}{2015}}}$ | D. | $y={x^{-\frac{2015}{2016}}}$ |
分析 可对函数求导数,根据导数在(-∞,0)上的符号便可判断函数在(-∞,0)上的单调性,从而可判断选项A,B,C的正误,而选项D中的函数显然在(-∞,0)上不存在,这样便可找出正确选项.
解答 解:A.$y′=\frac{2016}{2015}{x}^{\frac{1}{2015}}$;
∵x<0;
∴${x}^{\frac{1}{2015}}<0$;
∴y′<0;
∴该函数在(-∞,0)上为减函数,∴该选项正确;
B.$y′=\frac{2013}{2015}{x}^{-\frac{2}{2015}}$;
∵x<0;
∴${x}^{-\frac{2}{2015}}>0$;
∴y′>0;
∴该函数在(-∞,0)上为增函数,∴该选项错误;
C.$y′=-\frac{2014}{2015}{x}^{-\frac{4029}{2015}}$;
∵x<0;
∴${x}^{-\frac{4029}{2015}}<0$;
∴y′>0;
∴该函数在(-∞,0)上为增函数,∴该选项错误;
D.x<0时,函数$y={x}^{-\frac{2015}{2016}}$无意义,∴该选项错误.
故选:A.
点评 考查根据导数符号判断函数单调性的方法,能将分数指数幂变成根式,从而判断该分数指数幂的符号,注意正确求导.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
8.已知数列{an}是以a为首项,a为公比的等比数列(a>0,a≠1),令bn=an1gan,若{bn}中的每一项总小于它后面的一项,则a的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (1,+∞) | C. | (0,$\frac{1}{2}$)∪(1,+∞) | D. | (0,1)∪(1,+∞) |
20.若椭圆${x^2}+\frac{y^2}{2}=1$的两个焦点是F1,F2,点P在椭圆上,且PF1⊥F1F2,那么|PF2|=( )
| A. | 2 | B. | 4 | C. | $\frac{5}{2}\sqrt{2}$ | D. | $\frac{3}{2}\sqrt{2}$ |
14.化简$\frac{sinθ}{{\sqrt{1-{{sin}^2}θ}}}+\frac{{\sqrt{1-{{cos}^2}θ}}}{cosθ}(\frac{π}{2}<θ<π)$的结果是( )
| A. | 0 | B. | 2tanθ | C. | -2tanθ | D. | $\frac{1}{2tanθ}$ |
18.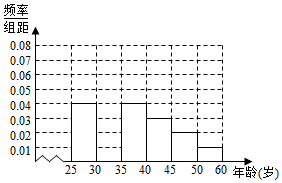 某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为:非低碳族“,得到如下统计表和各年龄段人数频率分布直方图:
某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为:非低碳族“,得到如下统计表和各年龄段人数频率分布直方图:
(1)补全频率分布直方图,并求n,a,p的值;
(2)从[40,50)岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取3人作为领队,求选取的3名领队中年龄都在[40,45)岁的概率.
 某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为:非低碳族“,得到如下统计表和各年龄段人数频率分布直方图:
某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为:非低碳族“,得到如下统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 低碳族 的人数 | 占本组 的频率 |
| 1 | [25,30) | 120 | 0.6 |
| 2 | [30,35) | 195 | P |
| 3 | [35,40) | 100 | 0.5 |
| 4 | [40,45) | a | 0.4 |
| 5 | [45,50) | 30 | 0.3 |
| 6 | [50,55) | 15 | 0.3 |
(2)从[40,50)岁年龄段的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取3人作为领队,求选取的3名领队中年龄都在[40,45)岁的概率.
19.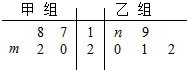 某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )
某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )
 某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )
某车间将10名工人评价分成甲、乙两组加工某种零件,在单位时间内每个工人加工的合格零件数如茎叶图所示.已知两组工人在单位时间内加工的合格零件平均数都为20,则有( )| A. | m=3,n=8 | B. | m=4,n=7 | C. | m=5,n=6 | D. | m=6,n=5 |