题目内容
已知 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且 在区间[-1,4]上的最大值是12.
在区间[-1,4]上的最大值是12.
(1)求f(x)的解析式;
(2)是否存在正整数m,使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
(1) ;(2)方程
;(2)方程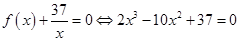 ,
,
设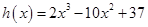 ,则
,则 .
.
当 时,
时,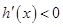 ,
, 是减函数;当
是减函数;当 时,
时,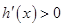 ,
, 是增函数.
是增函数.
因为 .所以方程
.所以方程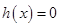 在区间
在区间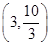 ,
, 内分别有唯一实数根,而区间
内分别有唯一实数根,而区间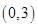 ,
,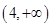 内没有实数根.所以存在唯一的正数
内没有实数根.所以存在唯一的正数 ,使得方程
,使得方程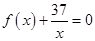 在区间
在区间 内有且只有两个不等的实数根.
内有且只有两个不等的实数根.
解析试题分析:(1)由已知得0,5是二次函数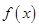 的两个零点值,所以可设
的两个零点值,所以可设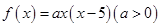 ,开口方向向上,对称轴为
,开口方向向上,对称轴为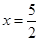 ,因此
,因此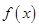 在区间
在区间 上的最大值是
上的最大值是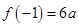 ,则
,则 ,即
,即 ,因此可求出函数
,因此可求出函数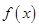 的解析式;(2)由(1)得
的解析式;(2)由(1)得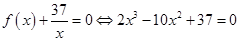 ,构造函数
,构造函数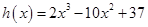 ,则方程
,则方程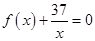 的实数根转化为函数
的实数根转化为函数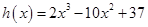 的零点,利用导数法得到函数
的零点,利用导数法得到函数 减区间为
减区间为 、增区间为
、增区间为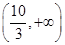 ,又有
,又有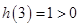 ,
,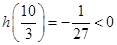 ,
,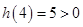 ,发现函数
,发现函数 在区间
在区间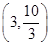 ,
, 内分别有唯一零点,而在区间
内分别有唯一零点,而在区间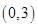 ,
,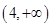 内没有零点,所以存在唯一的正数
内没有零点,所以存在唯一的正数 ,使得方程
,使得方程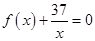 在区间
在区间 内有且只有两个不等的实数根.
内有且只有两个不等的实数根.
(1)因为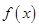 是二次函数,且
是二次函数,且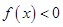 的解集是
的解集是 ,
,
所以可设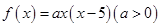 2分
2分
所以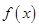 在区间
在区间 上的最大值是
上的最大值是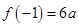 . 4分
. 4分
由已知,得 ,
,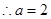 .
.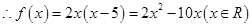 . 6分
. 6分
(2)方程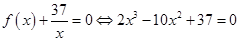 ,
,
设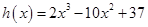 ,则
,则 . 10分
. 10分
当 时,
时,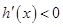 ,
, 是减函数;
是减函数;
当 时,
时,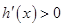 ,
, 是增函数. 10分
是增函数. 10分
因为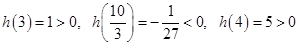 .
.
所以方程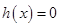 在区间
在区间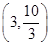 ,
, 内分别有唯一实数根,而区间
内分别有唯一实数根,而区间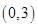 ,
,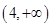 内没有实数根. 12分
内没有实数根. 12分
所以存在唯一的正数 ,使得方程
,使得方程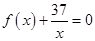 在区间
在区间 内有且只有两个不等的实数根. 14分
内有且只有两个不等的实数根. 14分
考点:1.函数解析式;2.函数零点.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
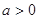 且
且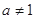 ,函数
,函数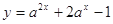 在
在 的最大值是14,求
的最大值是14,求 的值。
的值。 ,分别求f1(x)和f2(x);
,分别求f1(x)和f2(x);
 .
. 的奇偶性;
的奇偶性; 上为减函数,求
上为减函数,求 的取值范围.
的取值范围. 中,
中, 为奇数,
为奇数, 均为整数,且
均为整数,且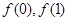 均为奇数.求证:
均为奇数.求证: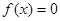 无整数根。
无整数根。 的三内角分别为
的三内角分别为 ,向量
,向量

 ,记函数
,记函数 .
.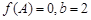 ,求
,求 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;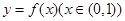 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求 的充要条件;
的充要条件; .
. ,不等式
,不等式 的解集为
的解集为 .
. 的值;
的值; 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.