题目内容
已知 的三内角分别为
的三内角分别为 ,向量
,向量

 ,记函数
,记函数 .
.
(1)若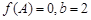 ,求
,求 的面积;
的面积;
(2)若关于 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
(1)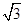 ;(2)
;(2)
解析试题分析:(1)由数量积的坐标运算,将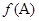 表示为
表示为 ,然后利用
,然后利用 ,将其转换为关于
,将其转换为关于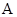 的一元函数,并将其变形为
的一元函数,并将其变形为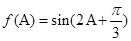 ,计算
,计算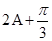 的范围,又
的范围,又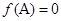 ,从而可求出
,从而可求出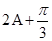 的值,进而确定
的值,进而确定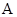 ,从而可求
,从而可求 的面积;(2) 方程
的面积;(2) 方程 有两个不同的实数解,即函数
有两个不同的实数解,即函数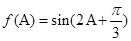 (
(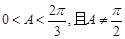 )的图象和直线
)的图象和直线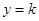 有两个不同的交点,为了便于画图象,可设
有两个不同的交点,为了便于画图象,可设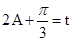 ,这样只需画
,这样只需画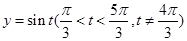 的图象和
的图象和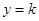 即可,从图象观察,可得实数
即可,从图象观察,可得实数 的取值范围.
的取值范围.
(1)由
即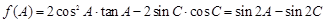 ,
,
又因为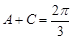 ,所以
,所以 代入上式得,
代入上式得,
由 ,得
,得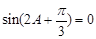 ,
,
又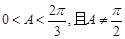 ,所以
,所以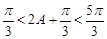 ,且
,且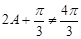 5分
5分
也所以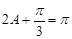 ,即
,即 ,从而
,从而 为正三角形,
为正三角形,
所以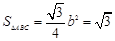 8分
8分
(2)由(1)知 ,令
,令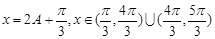 ,
,
则方程 有两个不同的实数解等价于
有两个不同的实数解等价于 在
在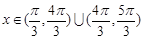 上有两上不同实根,作出
上有两上不同实根,作出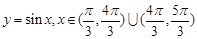 草图如右,
草图如右,
可知当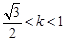 或
或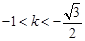 时,直线
时,直线 与曲线
与曲线 有两个交点,符合题意,故实数
有两个交点,符合题意,故实数 的取值范围为
的取值范围为 . 12分
. 12分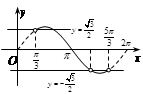
考点:1、平面向量的数量积运算;2、三角函数的图象和性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
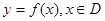 (
( 为定义域)图像上的点到坐标原点的距离为函数的
为定义域)图像上的点到坐标原点的距离为函数的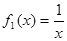 与
与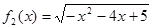 是否存在长距与短距,若存在,请求出;
是否存在长距与短距,若存在,请求出;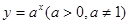 的短距小于1;
的短距小于1;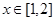 是否存在实数
是否存在实数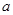 ,使得函数
,使得函数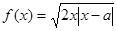 的短距不小于2且长距不大于4.若存在,请求出
的短距不小于2且长距不大于4.若存在,请求出 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且 在区间
在区间 内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由. .
. 为常数且
为常数且
 时,求
时,求 ;
; 满足
满足 ,但
,但 ,则称
,则称 的二阶周期点.证明函数
的二阶周期点.证明函数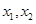 ;
;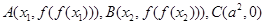 ,记
,记 的面积为
的面积为 ,求
,求 上的最大值和最小值。
上的最大值和最小值。
 .现已知相距18
.现已知相距18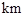 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设 (
( 的函数; (2)若
的函数; (2)若 ,且
,且 时,
时, 的值.
的值.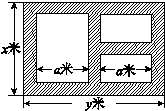
 .
. 在
在 上的最大值和最小值;
上的最大值和最小值; 时,函数
时,函数 的下方.
的下方.