题目内容
已知函数
(1)若函数 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;
(2)设函数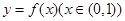 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求 的充要条件;
的充要条件;
(3)若函数 的图象上任意不同的两点的连线的斜率小于l,求证
的图象上任意不同的两点的连线的斜率小于l,求证 .
.
(1) ,
, ;(2)
;(2) ;(3)
;(3)
解析试题分析:(1)由函数 的图象切x轴于点(2,0),得
的图象切x轴于点(2,0),得 且
且 ,解方程组可得
,解方程组可得 的值.
的值.
(2)由于 ,根据导数的几何意义,任意不同的两点的连线的斜率小于l,
,根据导数的几何意义,任意不同的两点的连线的斜率小于l, 对任意的
对任意的 恒成立,利用分离变量法,转化为
恒成立,利用分离变量法,转化为 对任意的
对任意的 恒成立,进一步转化为函数的最值问题;
恒成立,进一步转化为函数的最值问题;
(3)设 ,则
,则

 对
对 恒成立
恒成立
将上不等式看成是关于 的一元二次不等式即可.
的一元二次不等式即可.
解:(1)
由 ,得
,得 ,
,
又 ,得
,得
(2)
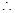 对任意的
对任意的 ,即
,即 对任意的
对任意的 恒成立
恒成立
等价于 对任意的
对任意的 恒成立
恒成立
令
则

 ,当且仅当
,当且仅当 时“=”成立,
时“=”成立,
 在
在 上为增函数,
上为增函数,

(3)设 ,则
,则
即 ,对
,对 恒成立
恒成立 ,对
,对 恒成立
恒成立
即 ,对
,对 恒成立
恒成立
解得
考点:1、导数的几何意义;2、等价转化的思想;3、二次函数与一元二次一不等式问题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
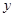 (单位:千克)与销售价格
(单位:千克)与销售价格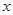 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式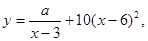 其中
其中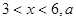 为常数。己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数。己知销售价格为5元/千克时,每日可售出该商品11千克. 的值;
的值; 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且 在区间
在区间 内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
内有且只有两个不等的实数根?若存在,求出所有m的值;若不存在,请说明理由.
 .现已知相距18
.现已知相距18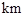 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设 (
( 的函数; (2)若
的函数; (2)若 ,且
,且 时,
时, 的值.
的值.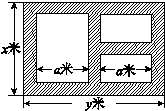

 .
. ,讨论函数
,讨论函数 在区间
在区间 上的单调性;
上的单调性; 且
且 ,对任意的
,对任意的 ,试比较
,试比较 的大小.
的大小. .
. 在
在 上的最大值和最小值;
上的最大值和最小值; 时,函数
时,函数 的下方.
的下方. ,若存在非零常数
,若存在非零常数 ,使函数
,使函数 ,都有
,都有 ,则称函数
,则称函数 为函数
为函数 称为周距.
称为周距. 是以2为广义周期的广义周期函数,并求出它的相应周距
是以2为广义周期的广义周期函数,并求出它的相应周距 ,使
,使 (
( 为常数,
为常数, )为广义周期函数,并求出它的一个广义周期
)为广义周期函数,并求出它的一个广义周期 的周期函数,当函数
的周期函数,当函数 在
在 上的值域为
上的值域为 时,求
时,求 上的最大值和最小值.
上的最大值和最小值. .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的图象在区间
的图象在区间 上有公共点,求实数
上有公共点,求实数 的取值范围.
的取值范围.