题目内容
已知数列 满足
满足 .
.
(1)求证:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式
的通项公式 ;
;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:对任意
,求证:对任意 ,有
,有 成立.
成立.
(1) ;(2)见解析。
;(2)见解析。
解析试题分析:(1)根据 对数列
对数列 的通项公式
的通项公式 进行配凑,根据定义去证明;(2)结合(1)及三角函数的周期性得
进行配凑,根据定义去证明;(2)结合(1)及三角函数的周期性得 然后放缩构造等比数列进行求和,
然后放缩构造等比数列进行求和,
(1)
又 数列
数列 是首项为3,公比为-2的等比数列. 4′
是首项为3,公比为-2的等比数列. 4′
从而 6′
6′
(2) 8′
8′
当 时,则
时,则

 12′
12′ 14′
14′
考点:(1)等比数列数列定义的应用;(2)放缩法证明不等式。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, =6,
=6, =5,则
=5,则 等于
等于  中,若
中,若
 ,设
,设 ,
, 是等比数列;
是等比数列; 的前n项和
的前n项和 与通项
与通项 满足
满足 .
. ,求
,求 ;
; ,求
,求 的前n项和
的前n项和 .
. ;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来
;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来 的线段,且这两条线段与原线段两两夹角为
的线段,且这两条线段与原线段两两夹角为 级分形图.
级分形图.
 的前
的前 项和
项和 .
. ,都有
,都有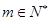 ,使得
,使得 成等比数列.
成等比数列. 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且 ,
,
 求数列
求数列 的前
的前 项和
项和 .
. 的前
的前 项和为
项和为 满足
满足 .
. 的前
的前 .
. 的前
的前 项和
项和 满足:
满足: (
( 为常数,
为常数,
 的通项公式;
的通项公式; ,若数列
,若数列 为等比数列,求
为等比数列,求