题目内容
已知直线y=kx+1，抛物线x2=ay（a≠0），无论k取何值，直线与抛物线恒有公共点，则a的取值范围（ ）
| A、（-∞，+∞） |
| B、（-∞，0） |
| C、（0，+∞） |
| D、[-4，0）∪（0，4] |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由直线y=kx+1，抛物线x2=ay（a≠0），无论k取何值，直线与抛物线恒有公共点，得到由函数解析式组成的方程有实数解，然后利用判别式即可得到关于k的方程，即可解决问题．
解答：
解：直线y=kx+1代入抛物线x2=ay可得x2-akx-a=0，
∴△=a2k2+4a≥0
∵无论k取何值，直线与抛物线恒有公共点，
∴a＞0，
故选：C．
∴△=a2k2+4a≥0
∵无论k取何值，直线与抛物线恒有公共点，
∴a＞0，
故选：C．
点评：此题主要考查了抛物线与直线的交点及一元二次方程的判别式，解题时首先根据直线与抛物线有交点利用判别式得到关于k的不等式，解表达式即可解决问题．
练习册系列答案
相关题目
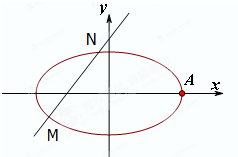如图，已知点A是椭圆
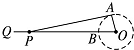如图为曲柄连杆结构示意图，当曲柄 OA 在 OB 位置时，连杆端点 P 在 Q 的位置，当 OA 自 OB 按顺时针旋转 α 角时，P 和 Q 之间的距离为 x，已知 OA=25cm，AP=125cm，若 OA⊥AP，则 x 等于
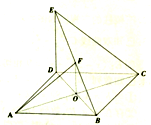如图，菱形ABCD的边长为2，对角线交于点O，DE⊥平面ABCD；