题目内容
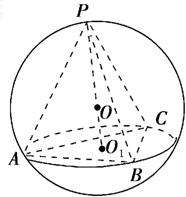 三棱锥P-ABC的四个顶点都在体积为
三棱锥P-ABC的四个顶点都在体积为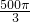 的球的表面上,底面ABC所在的小圆面积为16π,则该三棱锥的高的最大值为
的球的表面上,底面ABC所在的小圆面积为16π,则该三棱锥的高的最大值为
- A.7
- B.7.5
- C.8
- D.9
C
分析:由球的体积为 ,可以得球的半径;由小圆面积为16π,可以得小圆的半径;由图知三棱锥高的最大值应过球心,故可以作出解答.
,可以得球的半径;由小圆面积为16π,可以得小圆的半径;由图知三棱锥高的最大值应过球心,故可以作出解答.
解答:如图,设球的半径为R,由球的体积公式得: πR3=
πR3= π,∴R=5.
π,∴R=5.
又设小圆半径为r,则πr2=16π,∴r=4.
显然,当三棱锥的高过球心O时,取得最大值;
由OO1= =3,所以高PO1=PO+OO1=5+3=8.
=3,所以高PO1=PO+OO1=5+3=8.
故选C.
点评:本题考查了由球的体积求半径,由圆的面积求半径,以及勾股定理的应用,是基础题.
分析:由球的体积为
 ,可以得球的半径;由小圆面积为16π,可以得小圆的半径;由图知三棱锥高的最大值应过球心,故可以作出解答.
,可以得球的半径;由小圆面积为16π,可以得小圆的半径;由图知三棱锥高的最大值应过球心,故可以作出解答.解答:如图,设球的半径为R,由球的体积公式得:
 πR3=
πR3= π,∴R=5.
π,∴R=5.
又设小圆半径为r,则πr2=16π,∴r=4.
显然,当三棱锥的高过球心O时,取得最大值;
由OO1=
 =3,所以高PO1=PO+OO1=5+3=8.
=3,所以高PO1=PO+OO1=5+3=8.故选C.
点评:本题考查了由球的体积求半径,由圆的面积求半径,以及勾股定理的应用,是基础题.

练习册系列答案
相关题目
 三棱锥P-ABC的四个顶点都在体积为
三棱锥P-ABC的四个顶点都在体积为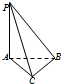 已知如图在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,PA=AC=BC=1,若三棱锥P-ABC的四个顶点都在某一个球面上,则该球的表面积为( )
已知如图在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,PA=AC=BC=1,若三棱锥P-ABC的四个顶点都在某一个球面上,则该球的表面积为( )