题目内容
7.已知定义在R上的函数y=f(x)是偶函数,且当x≥0时,f(x)=2x-1.(I)当x∈[-1,m](m>-1)时,求f(x)的值域;
(Ⅱ)x∈[a,b],函数的值域为[$\frac{1}{2}$,2],求实数a,b满足的条件.
分析 (I)根据函数奇偶性的,利用对称性求出函数f(x)的解析式,利用函数的单调性,结合函数的图象即可当x∈[-1,m](m>-1)时,求f(x)的值域;
(Ⅱ)根据函数值域,求出函数值对应的变量,结合函数的值域建立条件关系即可得到结论.
解答 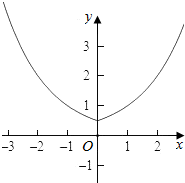 解:(I)若x<0,则-x>0,
解:(I)若x<0,则-x>0,
则f(-x)=2-x-1.
∵函数y=f(x)是偶函数,
∴f(-x)=2-x-1=f(x),
即f(x)=2-x-1,x<0.
当x=-1时,f(-1)=20=1,
当x≥0时,由f(x)=2x-1=1,得x-1=0,解得x=1,
当-1<m<0时,函数f(x)的最大值为f(-1)=1,最小值为f(m)=2-m-1,此时值域为[2-m-1,1],
当0≤m≤1时,函数f(x)的最大值为f(-1)=1,最小值为f(0)=$\frac{1}{2}$,此时值域为[$\frac{1}{2}$,1],
当m>1时,函数f(x)的最大值为f(m)=2m-1,最小值为f(0)=$\frac{1}{2}$,此时值域为[$\frac{1}{2}$,2m-1];
(Ⅱ)f(0)=$\frac{1}{2}$,由2x-1=2,得x-1=1,即x=2,由2-x-1=2,得-x-1=1,即x=-2,
若x∈[a,b],函数的值域为[$\frac{1}{2}$,2],
则0∈[a,b],且a=-2,或b=2,
若a=-2,则0≤b≤2,
若b=2,则-2≤a≤0.
点评 本题主要考查函数奇偶性的应用,以及函数值域的求解,利用函数图象结合函数单调性的性质是解决本题的关键.注意要进行分类讨论.

练习册系列答案
相关题目
18.函数y=$\sqrt{9-{3^x}}$的值域是( )
| A. | [0,+∞) | B. | [0,3] | C. | [0,3) | D. | (0,3) |
 如图所示,O是平行四边形ABCD所成平面外一点,若OA=9,OB=$\sqrt{61}$,CD=4,求异面直线OA与CD所成的角.
如图所示,O是平行四边形ABCD所成平面外一点,若OA=9,OB=$\sqrt{61}$,CD=4,求异面直线OA与CD所成的角. 将钟表上的时针作为角的始边,分针作为终边,那么当钟表上显示8点零5分时,求时针与分针构成的角度.
将钟表上的时针作为角的始边,分针作为终边,那么当钟表上显示8点零5分时,求时针与分针构成的角度.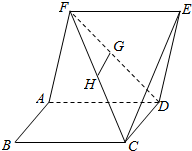 如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.
如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.