Question

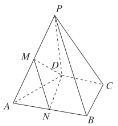
【题目】如图，把边长为4的正沿中位线折起使点到的位置.

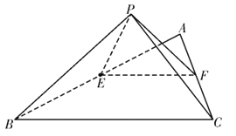
（1）在棱上是否存在点，使得平面？若存在，确定的位置，若不存在，说明理由；

（2）若，求四棱锥的体积.

Answer 1

【答案】（1）存在，是的中点；（2）3

【解析】

（1）取的中点，的中点，连接，，，利用三角形中位线定理，结合平行四边形的判定定理和性质定理、线面平行的判定定理进行推理论证即可；

（2）取的中点，的中点,可知、、三点共线，连接，，.利用线面垂直的判定定理和性质定理，结合勾股定理及逆定理、棱锥的体积公式进行求解即可.

（1）取的中点，的中点，连接，，，则是的中位线，∴，同理，∴.

∴四边形是平行四边形，∴，又面，面，

∴平面，∴上存在中点使平面.

（2）取的中点，的中点，易知、、三点共线，连接，，.

易知，∴，

又.

∴面.

又，

∴面，

∴.

又，.

∴，

又易知，

∴，

∴，

又，

∴面.

∴.