题目内容
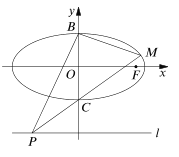
【题目】如图,已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,点
的上、下顶点,点![]() 是直线
是直线![]() 上的一个动点(与
上的一个动点(与![]() 轴的交点除外),直线
轴的交点除外),直线![]() 交椭圆于另一个点
交椭圆于另一个点![]() .
.
(1)当直线![]() 经过椭圆的右焦点
经过椭圆的右焦点![]() 时,求
时,求![]() 的面积;
的面积;
(2)①记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值;
为定值;
②求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)①见解析②
(2)①见解析②![]()
【解析】
试题(1)先联立直线![]() 的方程为
的方程为![]() 与椭圆方程
与椭圆方程![]() 的方程组,求出交点
的方程组,求出交点![]() 坐标
坐标![]() ,进而求出点到直线的距离公式求出上的高
,进而求出点到直线的距离公式求出上的高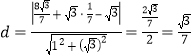 ,运用三角形的面积公式求解;(2)先求出斜率
,运用三角形的面积公式求解;(2)先求出斜率![]() 的值,再计算其积进行推算;先运用直线与椭圆的位置关系计算出向量的
的值,再计算其积进行推算;先运用直线与椭圆的位置关系计算出向量的![]() 的坐标形式,再运用向量的数量积公式进行推证:
的坐标形式,再运用向量的数量积公式进行推证:
解:(1)由题意![]() ,焦点
,焦点![]() ,
,
当直线![]() 过椭圆的右焦点
过椭圆的右焦点![]() 时,则直线
时,则直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
联立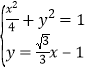 ,解得
,解得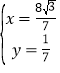 或
或![]() (舍),即
(舍),即![]() .
.
连![]() ,则直线
,则直线![]() ,即
,即 ![]() ,
,
而![]() ,
,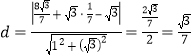 .
.
故![]() .
.
(2)解:法一:①设![]() ,且
,且![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
,
联立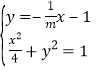 化简得
化简得![]() ,
,
解得![]() ,
,
所以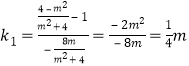 ,
,![]() ,
,
所以![]() 为定值.
为定值.
②由①知,![]() ,
,![]() ,
,
所以![]() ,
,
令![]()
故![]() ,
,
因为![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
解法二:①设点![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() .
.
所以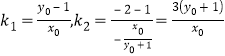 ,
,
所以![]() (定值).
(定值).
②由①知,![]() ,
,![]() ,
,
所以,![]()
![]() .
.
令![]() ,则
,则![]() ,
,
因为![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
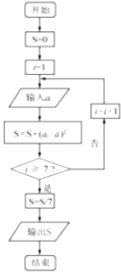
【题目】某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中 ![]() 是这7个数据的平均数),则输出的S的值是( )
是这7个数据的平均数),则输出的S的值是( )
观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |
A.1
B.![]()
C.![]()
D.![]()