题目内容
16.已知α,β均为锐角,且sin2α=2sin2β,则( )| A. | tan(α+β)=3tan(α-β) | B. | tan(α+β)=2tan(α-β) | C. | 3tan(α+β)=tan(α-β) | D. | 3tan(α+β)=2tan(α-β) |
分析 利用sin2α=2sin2β,得到sin[(α+β)+(α-β)]=2sin[(α+β)-(α-β)],化简计算即可.
解答 解:∵sin2α=2sin2β,
∴sin[(α+β)+(α-β)]=2sin[(α+β)-(α-β)],
∴sin(α+β)cos(α-β)+cos(α+β)sin(α-β)=2sin(α+β)cos(α-β)-2cos(α+β)sin(α-β),
∴3cos(α+β)sin(α-β)=sin(α+β)cos(α-β),
∴tan(α+β)=3tan(α-β),
故选:A
点评 本题考查了三角函数的化简,以及两角和与差的正弦公式和同角的三角函数的关系,属于基础题

练习册系列答案
相关题目
6.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,其焦距为2c,点Q(c,$\frac{a}{2}$)在椭圆的内部,点P是椭圆C上的动点,且|PF1|+|PQ|<5|F1F2|恒成立,则椭圆离心率的取值范围是( )
| A. | ($\frac{1}{5}$,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{1}{4}$,$\frac{\sqrt{2}}{2}$) | C. | ($\frac{1}{3}$,$\frac{\sqrt{2}}{2}$) | D. | ($\frac{2}{5}$,$\frac{\sqrt{2}}{2}$) |
6.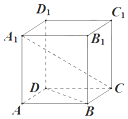 如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
 如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
 如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.