题目内容
17．函数f（x）=2x3+9x2-2在区间[-4，2]上的最大值和最小值分别为（ ）| A． | 25，-2 | B． | 50，14 | C． | 50，-2 | D． | 50，-14 |
分析 求导，分析出函数的单调性，进而求出函数的极值和两端点的函数值，可得函数f（x）=2x3+9x2-2在区间[-4，2]上的最大值和最小值．
解答 解：∵函数f（x）=2x3+9x2-2，
∴f′（x）=6x2+18x，
当x∈[-4，-3），或x∈（0，2]时，f′（x）＞0，函数为增函数；
当x∈（-3，0）时，f′（x）＜0，函数为减函数；
由f（-4）=14，f（-3）=25，f（0）=-2，f（2）=50，
故函数f（x）=2x3+9x2-2在区间[-4，2]上的最大值和最小值分别为50，-2，
故选：C．
点评 本题考查的知识点是利用导数求闭区间上的函数的最值，难度中档．
练习册系列答案
相关题目
7．若变量x，y满足$\left\{{\begin{array}{l}{x+y≤2}\\{2x-3y≤9}\\{x≥0}\end{array}}\right.$则z=（x+1）2+y2的最大值是（ ）
| A． | 12 | B． | 10 | C． | 17 | D． | 26 |
12．以点（2，-1）为圆心，且被直线x+y-6=0截得弦长为$\sqrt{30}$的圆的方程是（ ）
| A． | （x+2）2+（y-1）2=40 | B． | （x-2）2+（y+1）2=40 | C． | （x+2）2+（y-1）2=20 | D． | （x-2）2+（y+1）2=20 |
如图，在救灾现场，搜救人员从A点出发沿正北方向行进x米到达B处，探测到一个生命迹象，然后从B处沿南偏东75°行进30米到达C处，探测到另一个生命迹象，如果C处恰好在A处的北偏东60°方向上，那么x=10$\sqrt{6}$．米．
9．已知函数f（x）=kx2-3x+1的图象与x轴在原点的右侧有公共点，则实数k的取值范围为（ ）
| A． | （0，$\frac{9}{4}$） | B． | [0，$\frac{9}{4}$] | C． | （-∞，$\frac{9}{4}$） | D． | （-∞，$\frac{9}{4}$] |
6．
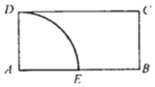如图，在矩形ABCD中，AD=1，AB=2，以A为圆心，AD为半径在矩形内部作扇形AED，若向矩形ABCD内部随机投放一点，则所投点落在扇形外部的概率为（ ）
如图，在矩形ABCD中，AD=1，AB=2，以A为圆心，AD为半径在矩形内部作扇形AED，若向矩形ABCD内部随机投放一点，则所投点落在扇形外部的概率为（ ）| A． | $\frac{π}{8}$ | B． | 1-$\frac{π}{8}$ | C． | $\frac{π}{4}$ | D． | 1-$\frac{π}{4}$ |
7．直线l1：（m-1）x+y=4m-1与直线l2：2x-3y=5互相平行的充要条件是（ ）
| A． | m=$\frac{2}{3}$ | B． | m=$\frac{1}{3}$ | C． | m=-$\frac{2}{3}$ | D． | m=-$\frac{1}{3}$ |