题目内容
已知函数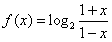
，x∈（- 1，1）。
（Ⅰ）判断f（x）的奇偶性，并证明；
（Ⅱ）判断f（x）在（-1，1）上的单调性，并证明。
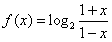，x∈（- 1，1）。（Ⅰ）判断f（x）的奇偶性，并证明；
（Ⅱ）判断f（x）在（-1，1）上的单调性，并证明。
解：（Ⅰ）∵ｘ∈（-1，1），且对定义域内的任意ｘ均有：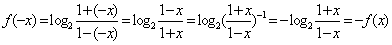 
，
∴函数f（x）是定义域内的奇函数。
（Ⅱ）任取 -1＜x1＜x2＜1，
则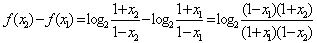
，
∵1-x1＞1-x2＞0，1+x2＞1+x1＞0，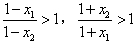
，
∴
，
∴
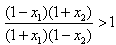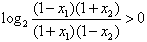，即
，
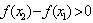∴函数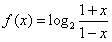
在（-1，1）上是增函数。
练习册系列答案
相关题目
已知函数f(x)=
，则它是（ ）
| ||
| |x-3|-3 |
| A、奇函数 | B、偶函数 |
| C、既奇又偶函数 | D、非奇非偶函数 |
已知函数f(x)=
则“-2≤a≤0”是“f（x）在R上单调递增”的（ ）
|
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |