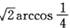题目内容
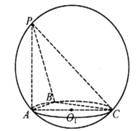
三棱锥P-ABC内接于球O,PA=PB=PC= ,侧棱PA、与底面ABC所成的角为60°,则该三棱锥的底面三角形ABC所在的截面圆面积为________.
,侧棱PA、与底面ABC所成的角为60°,则该三棱锥的底面三角形ABC所在的截面圆面积为________.
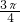
分析:过点P作PH⊥平面ABC于H,可得∠PAH是直线PA与底面ABC所成的角,得∠PAH=60°,从而可得底面三角形ABC所在的截面圆的半径,即可求得结论.
解答:
 过点P作PH⊥平面ABC于H,则
过点P作PH⊥平面ABC于H,则∵PA=PB=PC=
 ,
,∴H是三角形ABC的外心
∵AH是PA在平面ABC内的射影
∴∠PAH是直线PA与底面ABC所成的角,得∠PAH=60°,
∴Rt△PAH中,AH=PAcos60°=
 ,
,∴底面三角形ABC所在的截面圆的半径为

∴面积为
 =
=
故答案为:

点评:本题考查了直线与平面所成角的定义、球内接多面体,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 已知三棱锥P-ABC内接于球,三条侧棱两两垂直且长都为1,求球的表面积与体积.
已知三棱锥P-ABC内接于球,三条侧棱两两垂直且长都为1,求球的表面积与体积.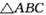 的外接圆为球O的小 圆
的外接圆为球O的小 圆 ,AB=1,PA=2.则下列结论正确的是
,AB=1,PA=2.则下列结论正确的是