题目内容
14.已知函数f(x)=x2-cosx,对于$[-\frac{π}{2},\frac{π}{2}]$上的任意x1,x2,有如下条件:①x1>x2;②x12>x22;③|x1|>x2;④x1+x2<0;⑤x1>|x2|.
其中能使f(x1)>f(x2)恒成立的条件序号是②.
分析 函数f(x)=x2-cosx为偶函数,f′(x)=2x+sinx,从面临是到函数f(x)在[0,$\frac{π}{2}$]上为单调增函数,在[-$\frac{π}{2}$,0]上为减函数.由此能求出结果.
解答 解:函数f(x)=x2-cosx为偶函数,f′(x)=2x+sinx,
当0<x≤$\frac{π}{2}$时,0<sinx≤1,0<2x≤π,
∴f′(x)>0,函数f(x)在[0,$\frac{π}{2}$]上为单调增函数,
由偶函数性质知函数在[-$\frac{π}{2}$,0]上为减函数.
当x12>x22时,得|x1|>|x2|≥0,
∴f(|x1|)>f(|x2|),
由函数f(x)在上[-$\frac{π}{2}$,$\frac{π}{2}$]为偶函数得f(x1)>f(x2),故②成立;
∵$\frac{π}{3}$>-$\frac{π}{3}$,而f($\frac{π}{3}$)=f(-$\frac{π}{3}$),
∴①不成立,同理可知③和⑤均不成立;
∵取x1=-$\frac{π}{3}$,x2=-$\frac{π}{2}$,满足x1+x2<0,但f(x1)<f(x2),故④不成立.
故能使f(x1)>f(x2)恒成立的条件序号②.
故答案为:②.
点评 本题考查能使不等式恒成立的条件的判断,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
5.已知cos$\frac{4π}{5}cos\frac{7π}{15}-sin\frac{9π}{5}$sin$\frac{7π}{15}$=cos(x+$\frac{π}{2}$)cosx+$\frac{2}{3}$,则sin2x等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{12}$ | D. | -$\frac{1}{12}$ |
2.下列几何体的截面图不可能是四边形的是( )
| A. | 圆柱 | B. | 圆锥 | C. | 圆台 | D. | 棱台 |
19.定义在R上的函数f(x)满足f(0)=0,f(x)+f(1-x)=1,$f(\frac{x}{3})=\frac{1}{2}f(x)$,且当0≤x1<x2≤1时,有f(x1)≤f(x2),则$f(\frac{1}{2016})$=( )
| A. | $\frac{1}{32}$ | B. | $\frac{1}{64}$ | C. | $\frac{1}{128}$ | D. | $\frac{1}{2016}$ |
4.函数f(x)是定义在(0,+∞)上的非负可导函数,且满足f(x)+xf'(x)≤0.对任意正数a、b,若a<b,则必有( )
| A. | af(b)≤bf(a) | B. | bf(a)≤af(b) | C. | af(a)≤bf(b) | D. | bf(b)≤af(a) |
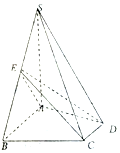 如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是边SB的中点.
如图,已知四棱锥S-ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD,E是边SB的中点.