题目内容
【题目】某公司为强化自己的市场竞争地位,决定扩大公司规模,拓展业务,建立连锁公司,连锁公司利润的20%归总公司,建立连锁公司的数量与单个公司月平均利润的关系如下表所示:
连锁公司数量 | 5 | 6 | 7 | 8 | 9 |
单个公司月平均利润 | 8 | 6 | 4.5 | 3.5 | 3 |
由相关系数![]() 可以反映两个变量相关性的强弱,
可以反映两个变量相关性的强弱,![]() ,认为变量相关性很强;
,认为变量相关性很强;![]() ,认为变量相关性一般;
,认为变量相关性一般;![]() ,认为变量相关性较弱.
,认为变量相关性较弱.
(1)计算相关系数![]() ,并判断变量
,并判断变量![]() 、
、![]() 相关性强弱;
相关性强弱;
(2)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程
(3)若一个地区连锁公司的前期投入![]() (十万元)与数量
(十万元)与数量![]() 的关系为
的关系为![]() ,根据所求回归方程从公司利润角度帮公司对一个地区连锁公司数量做出决策.
,根据所求回归方程从公司利润角度帮公司对一个地区连锁公司数量做出决策.
附注:参考数据:![]() ,
,
参考公式:相关系数 ,
,
线性回归方程![]() 中,
中,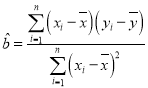 ,
,![]() .
.
【答案】(1)![]() ,变量
,变量![]() 、
、![]() 相关性很强;(2)
相关性很强;(2)![]() ;(3)6个
;(3)6个
【解析】
(1)根据给出的数据和公式,求出相关系数![]() ,并判断变量
,并判断变量![]() 、
、![]() 相关性强弱;
相关性强弱;
(2)根据给出的数据和公式,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)将总公司利润表过出来,再根据何时取最大值,帮公司对一个地区连锁公司数量做出决策.
(1)由题![]() ,
,![]()
则![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
则
![]()
![]() ,
,
则![]() ,变量
,变量![]() 、
、![]() 相关性很强;
相关性很强;
(2)由题
![]() ,
,
又![]()
![]() ,
,
故![]() .
.
(3)总公司利润![]()
![]()
![]()
![]()
![]() ,
,
即![]() ,
,![]()
对称轴为![]() ,故当
,故当![]() 时,总公司利润利润最大,
时,总公司利润利润最大,
故公司对一个地区连锁公司数量为6个.

【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)为了迎接春节,商场进行让利活动,一次购物款![]() 元及以上的一次返利
元及以上的一次返利![]() 元;一次购物不超过
元;一次购物不超过![]() 元的按购物款的百分比返利,具体见下表:
元的按购物款的百分比返利,具体见下表:
一次购物款(单位:元) |
|
|
|
|
返利百分比 |
|
|
|
|
请问该商场日均大约让利多少元?