题目内容
5.在直角三角形ABC中,∠C=90°,E,F是斜边AB的两个三等分点,且AC=6,BC=8,那么$\overrightarrow{CE}•\overrightarrow{CF}$=$\frac{200}{9}$.分析 可作出图形,根据向量加法及数乘的几何意义,并进行向量的数乘运算便可得出$\overrightarrow{CE}=\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB}$,$\overrightarrow{CF}=\frac{1}{3}\overrightarrow{CA}+\frac{2}{3}\overrightarrow{CB}$,而根据条件可求得${\overrightarrow{CA}}^{2}=36,{\overrightarrow{CB}}^{2}=64,\overrightarrow{CA}•\overrightarrow{CB}=0$,然后进行向量数量积的运算便可求出$\overrightarrow{CE}•\overrightarrow{CF}$的值.
解答 解:如图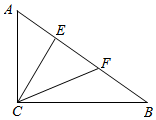
$\overrightarrow{CE}=\overrightarrow{CA}+\overrightarrow{AE}$=$\overrightarrow{CA}+\frac{1}{3}\overrightarrow{AB}$=$\overrightarrow{CA}+\frac{1}{3}(\overrightarrow{CB}-\overrightarrow{CA})$=$\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB}$;
$\overrightarrow{CF}=\overrightarrow{CA}+\frac{2}{3}(\overrightarrow{CB}-\overrightarrow{CA})$=$\frac{1}{3}\overrightarrow{CA}+\frac{2}{3}\overrightarrow{CB}$;
根据条件,${\overrightarrow{CA}}^{2}=36,{\overrightarrow{CB}}^{2}=64,\overrightarrow{CA}•\overrightarrow{CB}=0$;
∴$\overrightarrow{CE}•\overrightarrow{CF}=(\frac{2}{3}\overrightarrow{CA}+\frac{1}{3}\overrightarrow{CB})•(\frac{1}{3}\overrightarrow{CA}+\frac{2}{3}\overrightarrow{CB})$
=$\frac{2}{9}{\overrightarrow{CA}}^{2}+\frac{5}{9}\overrightarrow{CA}•\overrightarrow{CB}+\frac{2}{9}{\overrightarrow{CB}}^{2}$
=$8+0+\frac{128}{9}$
=$\frac{200}{9}$.
故答案为:$\frac{200}{9}$.
点评 考查向量加法和数乘的几何意义,以及向量的数乘运算,向量的数量积的运算,线段三等分点的概念,以及向量垂直的充要条件.

| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
| A. | y=sinx为增函数,y=cosx为增函数 | B. | y=sinx为减函数,y=cosx为减函数 | ||
| C. | y=sinx为增函数,y=cosx为减函数 | D. | y=sinx为减函数,y=cosx为增函数 |
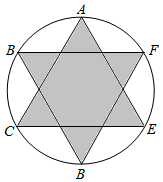 如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$.
如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$.