题目内容
以椭圆x2+| y2 | 2 |
分析:利用椭圆的方程中三个参数的关系求出其焦点坐标及顶点坐标;利用双曲线中三个参数的关系求出其中的参数b,写出双曲线的方程.
解答:解:∵x2+
=1的焦点为(0,±1),y轴上的两个顶点为(0,±
)
∴双曲线中a= 1,c=
∴b2=c2-a2=1
∴双曲线的方程为y2-x2=1
故答案为y2-x2=1
| y2 |
| 2 |
| 2 |
∴双曲线中a= 1,c=
| 2 |
∴b2=c2-a2=1
∴双曲线的方程为y2-x2=1
故答案为y2-x2=1
点评:解决圆锥曲线的方程问题一定要注意椭圆中三个参数的关系为:a2=b2+c2;双曲线中三个参数的关系为c2=b2+a2

练习册系列答案
相关题目
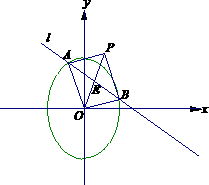 直线l:y=kx+1与椭圆C:
直线l:y=kx+1与椭圆C: