Question

直线l：y=kx+1与椭圆C：x2+

y2

2

=1交于A、B两点，以OA，OB为邻边作平行四边形
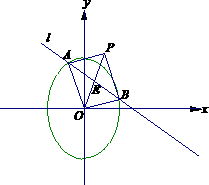
OAPB（O为坐标原点）（如图）．
（Ⅰ）当k=-1时，求AB的长；
（Ⅱ）当k变化时，求点P的轨迹方程．

Answer 1

分析：（Ⅰ）当k=-1时，直线与椭圆方程联立

y=-x+1 2x2+y2=2

，解之可求得A、B的坐标，从而可求AB的长；
（Ⅱ）设P（x，y），A（x₁，y₁），B（x₂，y₂），则E（

x

2

，

y

2

），联立方程组

y=kx+1 2x2+y2=2

，整理得（k²+2）x²+2kx-1=0，利用韦达定理可得x1+x2=-

2k

k2+2

，y1+y2=k(x1+x2)+2=

4

k2+2

，根据点E是AB的中点，可求点P的轨迹方程．

解答：解：（Ⅰ）当k=-1时，
联立方程组

y=-x+1 2x2+y2=2

，解之得

x=- 1 3 y= 4 3

或

x=1 y=0

，
即A、B的坐标分别为（-

1

3

，

4

3

）、（1，0）．
∴|AB|=

(1+ 1 3 )2+(0- 4 3 )2

=

4 2

3

．
（Ⅱ）设P（x，y），A（x₁，y₁），B（x₂，y₂），则E（

x

2

，

y

2

）．
联立方程组

y=kx+1 2x2+y2=2

，整理得（k²+2）x²+2kx-1=0，
由此得，x1+x2=-

2k

k2+2

，y1+y2=k(x1+x2)+2=

4

k2+2

由点E是AB的中点，有

x=- 2k k2+2 y= 4 k2+2

，
消去k得2x²+y²-2y=0，这就是点P的轨迹方程．

点评：本题主要考查直线与圆锥曲线的综合应用能力，涉及到轨迹方程的求法及直线与椭圆的相关知识，解题时要注意合理地进行等价转化