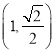题目内容
【题目】设
。
，
，
，
是
中的数所成的数列，它包含的不以1结尾的任何排列，即对于的四个数的任意一个不以1结尾的排列
，
，都有
，
，
，
，使得
，并且
，求这种数列的项数
的最小值。
【答案】11
【解析】
1.对于
，可以证明只有6项的数列中不可能含有
的任何排列。
2．对于
，证明只有11项的数列中不可能含有
的任何排列。
直接验证可知数列1，2，3，4，1，2，3，1，4，2，3，1包含
的任何排列，由此知12是最小值。
再回到问题本身，若有一个项数小于11的数列包含中不以1结尾的任何排列，则在此数列后再加上一个1，所得数列包含中的所有排列，但项数小于12，矛盾。另外，1，2，3，4，1，2，3，1，4，2，3包含了中不以1结尾的任何排列，故
的最小值为11.
练习册系列答案
相关题目
【题目】某果农从经过筛选（每个水果的大小最小不低于50克，最大不超过100克）的10000个水果中抽取出100个样本进行统计，得到如下频率分布表：
级别 | 大小（克） | 频数 | 频率 |
一级果 |
| 5 | 0.05 |
二级果 |
|
| |
三级果 |
| 35 |
|
四级果 |
| 30 | |
五级果 |
| 20 | |
合计 | 100 |
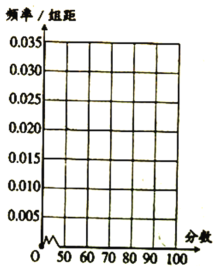
请根据频率分布表中所提供的数据，解得下列问题：
（1）求
的值，并完成频率分布直方图；
（2）若从四级果，五级果中按分层抽样的方法抽取5个水果，并从中选出2个作为展品，求2个展品中仅有1个是四级果的概率；
（3）若将水果作分级销售，预计销售的价格
元/个与每个水果的大小
克关系是：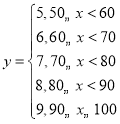
，则预计10000个水果可收入多少元？
