题目内容
.数列{an}满足an>0,前n项和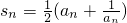 .
.
①求s1,s2,s3;
②猜想{sn}的通项公式,并用数学归纳法证明.
解:①由Sn= (an+
(an+ )得S1=
)得S1= (a1+
(a1+ ),
),
∴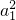 =1,又a1>0,
=1,又a1>0,
∴S1=a1=1,…(2分)
由S2=a1+a2
=1+a2
= (a2+
(a2+ )可得:
)可得: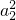 +2a2-1=0,a2>0,
+2a2-1=0,a2>0,
∴a2= -1,
-1,
∴S2= ,…(4分)
,…(4分)
同理可求a3= -
- ,S3=
,S3= …(6分)
…(6分)
∴s1=1,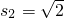 ,
,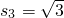 …(7分)
…(7分)
猜想Sn= ,下面用归纳法证明:
,下面用归纳法证明:
(1)当n=1时,s1=1显然猜想成立.…(9分)
(2)假设n=k时(k≥1)猜想也成立,
即sk= …(10分)
…(10分)
当n=k+1时,sk+1=sk+ak+1= +ak+1,
+ak+1,
又sk+1= (ak+1+
(ak+1+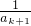 ),
),
∴ +ak+1=
+ak+1= (ak+1+
(ak+1+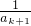 ),
),
∴ak+1=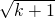 -
- ,
,
∴sk+1=sk+ak+1=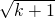 …(12分)
…(12分)
即n=k+1时猜想也成立.
由①,②得猜想成立.…(13分)
分析:①,由S1= (a1+
(a1+ ),a1>0可求得S1,从而可求得a2,继而可求得S2,S3;
),a1>0可求得S1,从而可求得a2,继而可求得S2,S3;
②由s1,s2,s3的值可猜得Sn= ,用数学归纳法证明即可.
,用数学归纳法证明即可.
点评:本题考查数列的递推公式,考查数学归纳法证明问题,猜得Sn= 是关键,考查分析与运算能力,属于中档题.
是关键,考查分析与运算能力,属于中档题.
 (an+
(an+ )得S1=
)得S1= (a1+
(a1+ ),
),∴
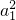 =1,又a1>0,
=1,又a1>0,∴S1=a1=1,…(2分)
由S2=a1+a2
=1+a2
=
 (a2+
(a2+ )可得:
)可得: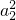 +2a2-1=0,a2>0,
+2a2-1=0,a2>0,∴a2=
 -1,
-1,∴S2=
 ,…(4分)
,…(4分)同理可求a3=
 -
- ,S3=
,S3= …(6分)
…(6分)∴s1=1,
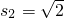 ,
,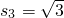 …(7分)
…(7分)猜想Sn=
 ,下面用归纳法证明:
,下面用归纳法证明:(1)当n=1时,s1=1显然猜想成立.…(9分)
(2)假设n=k时(k≥1)猜想也成立,
即sk=
 …(10分)
…(10分)当n=k+1时,sk+1=sk+ak+1=
 +ak+1,
+ak+1,又sk+1=
 (ak+1+
(ak+1+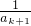 ),
),∴
 +ak+1=
+ak+1= (ak+1+
(ak+1+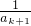 ),
),∴ak+1=
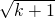 -
- ,
,∴sk+1=sk+ak+1=
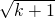 …(12分)
…(12分)即n=k+1时猜想也成立.
由①,②得猜想成立.…(13分)
分析:①,由S1=
 (a1+
(a1+ ),a1>0可求得S1,从而可求得a2,继而可求得S2,S3;
),a1>0可求得S1,从而可求得a2,继而可求得S2,S3;②由s1,s2,s3的值可猜得Sn=
 ,用数学归纳法证明即可.
,用数学归纳法证明即可.点评:本题考查数列的递推公式,考查数学归纳法证明问题,猜得Sn=
 是关键,考查分析与运算能力,属于中档题.
是关键,考查分析与运算能力,属于中档题. 
练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
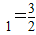 ,a
,a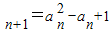 (n∈N*),则m=
(n∈N*),则m=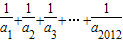 的整数部分是( )
的整数部分是( ) ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )
