题目内容
若用长度分别为1,1,1,1,x,x的六根笔直的铁棒通过焊接其端点(不计损耗)可以得到两种不同形状的三棱锥形的铁架,则实数x的取值范围是 .
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:根据题意,画出图形,分析底面边长是正三角形时构成三棱锥的情况,底面边长不是正三角形的情况,求出x的取值范围.
解答:
解:根据条件,四根长为1的直铁棒与两根长为x的直铁棒要组成三棱锥形的铁架,
有以下两种情况:
①底面是边长为1的正三角形,三条侧棱长为1,x,x,如图,
此时x应满足:∵AD=
,SD=
,且SD<SA+AD,
∴
<1+
,
即x2<2+
,
∴
<x<
;
②构成三棱锥的两条对角线长为x,其他各边长均为1,如图所示,
此时应满足0<x<
;
综上,x的取值范围是(0,
).
故答案为:(0,
).
有以下两种情况:
①底面是边长为1的正三角形,三条侧棱长为1,x,x,如图,

此时x应满足:∵AD=
| ||
| 2 |
x2-(
|
∴
x2-(
|
| ||
| 2 |
即x2<2+
| 3 |
∴
| 1 |
| 2 |
| ||||
| 2 |
②构成三棱锥的两条对角线长为x,其他各边长均为1,如图所示,

此时应满足0<x<
| 2 |
综上,x的取值范围是(0,
| ||||
| 2 |
故答案为:(0,
| ||||
| 2 |
点评:本题考查了空间想象能力与灵活运用知识解决数学问题的能力,解题时应分析底面边长是正三角形与底面边长不是正三角形的情况,是较难的题目.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
下列说法中正确的是( )
A、
| ||||||||
B、若
| ||||||||
C、若
| ||||||||
D、若
|

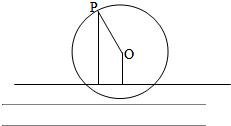 如图是一个半径为3米的水轮,水轮圆心O距离水面2米,已知水轮每分钟转动四圈,水轮上的点P相对于水面的高度y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2(A>0,ω>0,φ∈(-
如图是一个半径为3米的水轮,水轮圆心O距离水面2米,已知水轮每分钟转动四圈,水轮上的点P相对于水面的高度y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2(A>0,ω>0,φ∈(-