题目内容
(本题满分12分)
在平面直角坐标系xOy中,曲线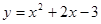 与坐标轴的交点都在圆C上。
与坐标轴的交点都在圆C上。
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C被直线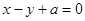 截得的弦长为
截得的弦长为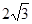 ,求
,求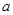 的值。
的值。
在平面直角坐标系xOy中,曲线
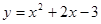 与坐标轴的交点都在圆C上。
与坐标轴的交点都在圆C上。(Ⅰ)求圆C的方程;
(Ⅱ)若圆C被直线
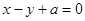 截得的弦长为
截得的弦长为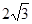 ,求
,求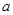 的值。
的值。(1) ;(Ⅱ)
;(Ⅱ) 。
。
 ;(Ⅱ)
;(Ⅱ) 。
。本试题主要是考查了圆的一般方程的求解,以及直线与圆相交的位置关系的综合运用。
(1)因为曲线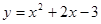 与坐标轴的交点为
与坐标轴的交点为 ,代入一般式中可知结论。
,代入一般式中可知结论。
(2)由(1)知圆心坐标为(-1,-1),半径为
则圆心到直线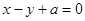 的距离为
的距离为 ,从而得到弦长的求解。
,从而得到弦长的求解。
解:(1)曲线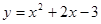 与坐标轴的交点为
与坐标轴的交点为 ……………………2分
……………………2分
设圆方程为 ,则:
,则:


 ……………………..5分
……………………..5分
 ……………………6分
……………………6分
(Ⅱ)由(1)知圆心坐标为(-1,-1),半径为 ………………8分
………………8分
则圆心到直线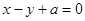 的距离为
的距离为 ……………….10分
……………….10分
由勾股定理知 解得
解得 ……………….12分
……………….12分
(1)因为曲线
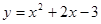 与坐标轴的交点为
与坐标轴的交点为 ,代入一般式中可知结论。
,代入一般式中可知结论。(2)由(1)知圆心坐标为(-1,-1),半径为

则圆心到直线
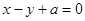 的距离为
的距离为 ,从而得到弦长的求解。
,从而得到弦长的求解。解:(1)曲线
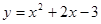 与坐标轴的交点为
与坐标轴的交点为 ……………………2分
……………………2分设圆方程为
 ,则:
,则:

 ……………………..5分
……………………..5分 ……………………6分
……………………6分(Ⅱ)由(1)知圆心坐标为(-1,-1),半径为
 ………………8分
………………8分则圆心到直线
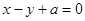 的距离为
的距离为 ……………….10分
……………….10分由勾股定理知
 解得
解得 ……………….12分
……………….12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
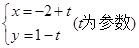 被圆
被圆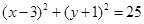 所截得的弦长为( )
所截得的弦长为( ) 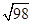
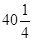
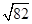
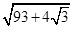
 中,圆
中,圆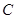 的方程为
的方程为 ,若直线
,若直线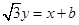 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆 的最大值是 ;
的最大值是 ; 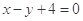 被圆
被圆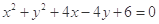 截得的弦长等于( )
截得的弦长等于( )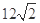
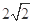
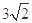
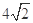
 内有一点P(-1,2),AB过点P
内有一点P(-1,2),AB过点P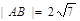 ,求直线AB的方程;
,求直线AB的方程;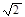 ,求直线AB的方程.
,求直线AB的方程. 上任意一点,则△ABC面积的最小值是______________.
上任意一点,则△ABC面积的最小值是______________.  ,(θ为参数)的位置关系是( )
,(θ为参数)的位置关系是( )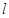 与圆
与圆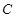 相交于点
相交于点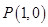 和点
和点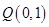 。
。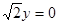 ,经过椭圆
,经过椭圆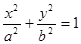 (a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为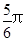 的直线l交椭圆于C、D两点.
的直线l交椭圆于C、D两点.