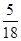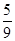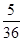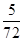题目内容
(本小题10分)圆 内有一点P(-1,2),AB过点P
内有一点P(-1,2),AB过点P
(1)若弦长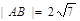 ,求直线AB的方程;
,求直线AB的方程;
(2)若圆上恰有三点到直线AB的距离等于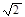 ,求直线AB的方程.
,求直线AB的方程.
 内有一点P(-1,2),AB过点P
内有一点P(-1,2),AB过点P(1)若弦长
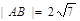 ,求直线AB的方程;
,求直线AB的方程;(2)若圆上恰有三点到直线AB的距离等于
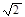 ,求直线AB的方程.
,求直线AB的方程.(1)倾斜角为60度或120度。(2)x-y+3=0或x+y-1=0。
本题考查弦长公式、点到直线的距离公式的应用,及用代定系数法求直线的斜率即直线方程.
①由弦长公式求出圆心到直线AB的距离,点斜式设出直线方程,由点到直线的距离公式求出斜率,再由斜率求倾斜角.
②由题意知,圆心到直线AB的距离d= 2,由点到直线的距离公式求出斜率,点斜式写出直线方程,并化为一般式.
解:圆心为C(-1,0),半径为 。
。
(1)设AB斜率为k,由AB方程为:y-2=k(x+1),即kx-y+k+2=0。
圆心C到AB的距离为:
而弦AB半弦长为 .
.
故: ,即
,即 ,
,
解得:
故:倾斜角为60度或120度。
(2)过C作AB的垂线,交AB于M,交圆于N。根据题意,MN= .
.
则: .即上述的
.即上述的 。所以:2/根号
。所以:2/根号
可得: 。
。
可求AB方程x-y+3=0或x+y-1=0。
①由弦长公式求出圆心到直线AB的距离,点斜式设出直线方程,由点到直线的距离公式求出斜率,再由斜率求倾斜角.
②由题意知,圆心到直线AB的距离d= 2,由点到直线的距离公式求出斜率,点斜式写出直线方程,并化为一般式.
解:圆心为C(-1,0),半径为
 。
。(1)设AB斜率为k,由AB方程为:y-2=k(x+1),即kx-y+k+2=0。
圆心C到AB的距离为:

而弦AB半弦长为
 .
.故:
 ,即
,即 ,
,解得:

故:倾斜角为60度或120度。
(2)过C作AB的垂线,交AB于M,交圆于N。根据题意,MN=
 .
.则:
 .即上述的
.即上述的 。所以:2/根号
。所以:2/根号
可得:
 。
。可求AB方程x-y+3=0或x+y-1=0。

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
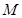 到点
到点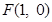 的距离,等于它到直线
的距离,等于它到直线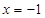 的距离.
的距离.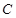 的方程;
的方程;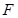 任意作互相垂直的两条直线
任意作互相垂直的两条直线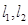 ,分别交曲线
,分别交曲线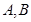 和
和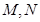 .设线段
.设线段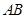 ,
,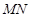 的中点分别为
的中点分别为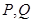 ,求证:直线
,求证:直线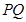 恒过一个定点;
恒过一个定点;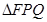 面积的最小值.
面积的最小值.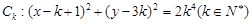 ,下列四个命题
,下列四个命题 和圆
和圆 相切,则实数
相切,则实数 的值是
的值是



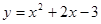 与坐标轴的交点都在圆C上。
与坐标轴的交点都在圆C上。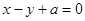 截得的弦长为
截得的弦长为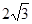 ,求
,求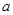 的值。
的值。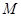 (1,3),与直线x+2y-7=0相切.
(1,3),与直线x+2y-7=0相切. 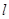 :
: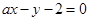
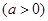 与圆C相交于A、B两点,求实数
与圆C相交于A、B两点,求实数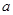 的取值范围;
的取值范围;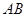 的垂直平分线过点
的垂直平分线过点 , 若存在,求出实数
, 若存在,求出实数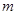 、
、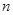 ,则直线
,则直线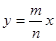 与圆
与圆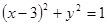 相交的概率是( )
相交的概率是( )