题目内容

10．函数y=ax-5+1（a＞0且a≠1）的图象必经过定点（　　）
A．（0，1）B．（5，1）C．（5，2）D．（1，5）

分析 由指数函数的定义可知，当指数为0时，指数式的值为1，故令指数x-5=0，解得x=5，y=2，故得定点（5，2）．

解答 解：令x-5=0，解得x=5，
此时y=a0+1=2，故得（5，2）
此点与底数a的取值无关，
故函数y=ax-5+1（a＞0且a≠1）的图象必经过定点（5，2）
故选：C．

点评 本题考点是指数型函数，考查指数型函数过定点的问题．解决此类题通常是令指数为0取得定点的坐标．属于指数函数性质考查题．

练习册系列答案
相关题目
20．求过两圆x2+y2-4y-6=0，x2+y2-5x+y-6=0交点且过（2，1）的圆的方程．
1．已知函数在R上是单调函数，f（x）=$\left\{\begin{array}{l}{（3a-1）x+4a，x＜1}\\{lo{g}_{a}x，x≥1}\end{array}\right.$，则实数a的取值范围是$\frac{1}{7}$≤a＜$\frac{1}{3}$．
18．某班有学生40人，将其数学成绩平均分为两组，第一组的平均分为80，标准差为4，第二组的平均分为90，标准差为6，则该班40名学生的数学成绩平均分为85，标准差为$\sqrt{51}$．
5．函数f（x）的定义域为A，若x1，x2∈A且f（x1）=f（x2）时总有x1=x2，则称f（x）为单函数．例如，函数f（x）=x+1（x∈R）是单函数．下列命题：①函数f（x）=x2-2x（x∈R）是单函数；②函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x≥2}\\{2-x，x＜2}\end{array}\right.$是单函数；③若f（x）为单函数，x1，x2∈A且x1≠x2，则f（x1）≠f（x2）；④函数f（x）在定义域内某个区间D上具有单调性，则f（x）一定是单函数．其中的真命题是③（写出所有真命题的编号）．
15．设a，b为实数，若复数$\frac{1+2i}{a+bi}$=1+i，则（　　）
A．a=1，b=3B．a=3，b=1C．a=$\frac{1}{2}$，b=$\frac{3}{2}$D．a=$\frac{3}{2}$，b=$\frac{1}{2}$
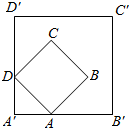2．如图所示，边长为1的正方形ABCD的顶点A，D分别在边长为2的正方形A′B′C′D′的边A′B′和A′D′上移动，则$\overrightarrow{A'B}•\overrightarrow{A'C}$的最大值是（　　）
A．2B．1+$\sqrt{2}$C．πD．4
19．设函数f（x）=$\frac{1}{2}$x2-2ax+（2a-1）lnx，其中a∈R．
（I）a=1时，求曲线y=f（x）在点（1，f（1））处的切线方程．
（Ⅱ）讨论函数y=f（x）的单调性．
20．圆（x-3）2+（y+1）2=1关于点（2，3）对称的曲线方程是（x-1）2+（y-7）2=1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网