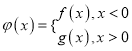题目内容
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,对任意正整数n,皆满足
,对任意正整数n,皆满足![]() (实常数
(实常数![]() ).在等差数
).在等差数![]() (
(![]() ))中,
))中,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)试判断数列![]() 能否成等比数列,并说明理由;
能否成等比数列,并说明理由;
(3)若![]() ,
,![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ,并计算:
,并计算:![]() (已知
(已知![]() ).
).
【答案】(1)![]() (2)见解析(3)
(2)见解析(3) ,
,![]()
【解析】
(1)因为对任意正整数n,皆满足![]() ,令
,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,又因为数列
,又因为数列![]() 是等差数列,则公差
是等差数列,则公差![]() ,数列
,数列![]() 的通项公式可求.
的通项公式可求.
(2)根据题意,![]() ,所以当
,所以当![]() 时,
时,![]() ,两式相减得:
,两式相减得:![]() .即数列
.即数列![]() 是等比数列,假设数列
是等比数列,假设数列![]() 能成等比数列,推出
能成等比数列,推出![]() ,矛盾,故假设错误,即数列
,矛盾,故假设错误,即数列![]() 不能成等比数列,
不能成等比数列,
(3)![]() ,故
,故![]() 的前n项和
的前n项和![]() 可以用错位相减法求,得到
可以用错位相减法求,得到![]() 的前n项和后再求其极限即可.
的前n项和后再求其极限即可.
解:(1)由![]() ,令
,令![]() 得,
得,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
等差数列![]() 的公差
的公差![]() .
.
所以数列![]() 的通项公式
的通项公式![]()
(2)因为对任意正整数n,皆满足![]() ,
,
所以当![]() 时,
时,![]() ,两式相减得:
,两式相减得:![]() .
.
即![]() ,所以数列是等比数列,公比为
,所以数列是等比数列,公比为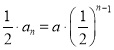 ,
, .
.
假设数列![]() 能成等比数列,则对任意正整数k,
能成等比数列,则对任意正整数k,![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() .显然不成立.
.显然不成立.
因此数列![]() 不可能为成等比数列.
不可能为成等比数列.
(用特殊的项加以说理亦可:例如,假设数列![]() 能成等比数列,则数列前3项也成等比,即
能成等比数列,则数列前3项也成等比,即![]() ,
,![]() ,因为
,因为![]() ,所以不成立)
,所以不成立)
(3)![]() ,
,
 ,
,
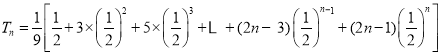 ,
,
上述两式相减得: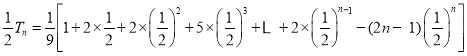 ,
,
所以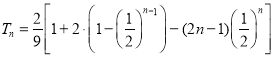 .
.
 ,
,
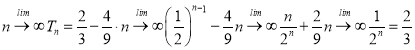 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目