题目内容
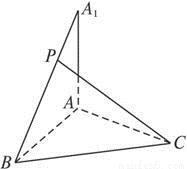
已知AA1⊥平面ABC,AB=BC=AA1=CA,P为A1B上的点.
(1)当![]() 为何值时,AB⊥PC;
为何值时,AB⊥PC;
(2)当二面角P-AC-B的大小为![]() 时,求
时,求![]() 的值.
的值.
解:(1)当![]() =1时.
=1时.

作PD∥A1A交AB于D,连CD.由A1A⊥面ABC,知PD⊥面ABC.当P为A1B中点时,D为AB中点.∵△ABC为正三角形,∴CD⊥AB.∴PC⊥AB(三垂线定理).
(2)过D作DE⊥AC于E,连结PE,则PE⊥AC,
∴∠DEP为二面角P—AC—B的平面角,∠DEP=![]() .
.
∴tan∠PED=![]() =
=![]() .
.
∴PD=![]() DE.∵DE=AD·sin60°=
DE.∵DE=AD·sin60°=![]() AD,∴PD=
AD,∴PD=![]() DE=
DE=![]() ×
×![]() AD=
AD=![]() AD.
AD.
又∵PD∥A1A,∴PD=BD.∴![]() .
.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
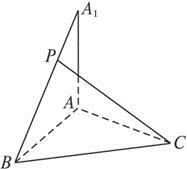 已知AA1⊥平面ABC,AB=BC=AA1=CA,P为A1B上的点.
已知AA1⊥平面ABC,AB=BC=AA1=CA,P为A1B上的点.
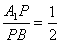 时,求二面角P-BC-A平面角的余弦值。
时,求二面角P-BC-A平面角的余弦值。 
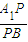 为何值时,AB⊥PC;
为何值时,AB⊥PC;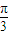 时,求
时,求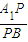 的值.
的值.