题目内容
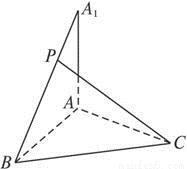
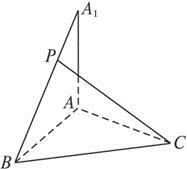 已知AA1⊥平面ABC,AB=BC=AA1=CA,P为A1B上的点.
已知AA1⊥平面ABC,AB=BC=AA1=CA,P为A1B上的点.(1)当
| A1P |
| PB |
(2)当二面角P-AC-B的大小为
| π |
| 3 |
| A1P |
| PB |
分析:(1)当
=1,作PD∥A1A交AB于D,连CD.由A1A⊥面ABC,知PD⊥面ABC,当P为A1B中点时,D为AB中点,而△ABC为正三角形,则CD⊥AB,根据三垂线定理可得PC⊥AB.
(2)过D作DE⊥AC于E,连接PE,则PE⊥AC,根据二面角平面角的定义可知∠DEP为二面角P-AC-B的平面角,在三角形PED中求出PD与DE的关系,根据DE=AD•sin60°=
AD,得到PD与AD的关系,而PD∥A1A,则PD=BD,从而求出
的值.
| A1P |
| PB |
(2)过D作DE⊥AC于E,连接PE,则PE⊥AC,根据二面角平面角的定义可知∠DEP为二面角P-AC-B的平面角,在三角形PED中求出PD与DE的关系,根据DE=AD•sin60°=
| ||
| 2 |
| A1P |
| PB |
解答:解:(1)当
=1时.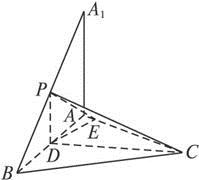 作PD∥A1A交AB于D,连CD.由A1A⊥面ABC,知PD⊥面ABC.
作PD∥A1A交AB于D,连CD.由A1A⊥面ABC,知PD⊥面ABC.
当P为A1B中点时,D为AB中点.
∵△ABC为正三角形,∴CD⊥AB.∴PC⊥AB(三垂线定理).
(2)过D作DE⊥AC于E,连接PE,则PE⊥AC,
∴∠DEP为二面角P-AC-B的平面角,∠DEP=
.
∴tan∠PED=
=
.
∴PD=
DE.
∵DE=AD•sin60°=
AD,
∴PD=
DE=
×
AD=
AD.
又∵PD∥A1A,
∴PD=BD.
∴
=
=
=
.
| A1P |
| PB |
 作PD∥A1A交AB于D,连CD.由A1A⊥面ABC,知PD⊥面ABC.
作PD∥A1A交AB于D,连CD.由A1A⊥面ABC,知PD⊥面ABC.当P为A1B中点时,D为AB中点.
∵△ABC为正三角形,∴CD⊥AB.∴PC⊥AB(三垂线定理).
(2)过D作DE⊥AC于E,连接PE,则PE⊥AC,
∴∠DEP为二面角P-AC-B的平面角,∠DEP=
| π |
| 3 |
∴tan∠PED=
| PD |
| DE |
| 3 |
∴PD=
| 3 |
∵DE=AD•sin60°=
| ||
| 2 |
∴PD=
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
又∵PD∥A1A,
∴PD=BD.
∴
| A1P |
| PB |
| AD |
| DB |
| AD |
| PD |
| 2 |
| 3 |
点评:本题主要考查了直线与平面垂直的性质,以及三垂线定理和与二面角有关的立体几何综合题,同时考查了学生计算能力、分析问题解决问题的能力,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
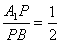 时,求二面角P-BC-A平面角的余弦值。
时,求二面角P-BC-A平面角的余弦值。 

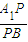 为何值时,AB⊥PC;
为何值时,AB⊥PC;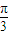 时,求
时,求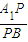 的值.
的值.