题目内容
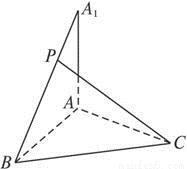
已知AA1⊥平面ABC，AB=BC=AA1=CA，P为A1B上的点.
（1）当
；
（2）当二面角P―AC―B的大小为
的值.
解法1：（1）当
时.
作PD∥A1A交AB于D，连CD.
由A1A⊥面ABC，知PD⊥面ABC.
当P为A1B中点时，D为AB中点.
∵△ABC为正三角形，
∴CD⊥AB，
∴PC⊥AB（三垂线定理）
（2）过D作DE⊥AC于E，连结PE，则PE⊥AC，
∴∠DEP为二面角P―AC―B的平面角，
，
又
解法2：建立空间直角坐标系如图所示，设AB=BC=AA1=CA=a.
则
设
（1）由
的中点，
即时，PC⊥AB.
（2）当
得，
设平面PAC的法向量
取
可设平面ABC的法向量为
（负值舍去）.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
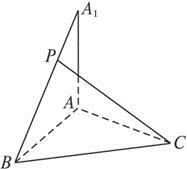已知AA1⊥平面ABC，AB=BC=AA1=CA，P为A1B上的点．
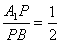时，求二面角P-BC-A平面角的余弦值。 
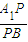为何值时,AB⊥PC；
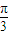时,求
的值.
为何值时，AB⊥PC；
时，求
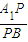的值．