题目内容
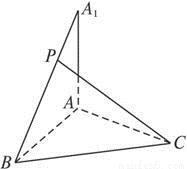
已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点。
(1)当P为A1B的中点时,求证:AB⊥PC ;
(2)当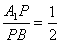 时,求二面角P-BC-A平面角的余弦值。
时,求二面角P-BC-A平面角的余弦值。
(2)当
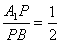 时,求二面角P-BC-A平面角的余弦值。
时,求二面角P-BC-A平面角的余弦值。 (1)证明:当 时,
时,
作PD∥AA1
由AA1
当P为A1B的中点时,D为AB中点,
∵△ABC为正三角形,
∴CD⊥AB,
∴AB⊥平面PCD,
∴PC⊥AB。
(2)解:过P作PD⊥AB于D,过D作DE⊥BC于E,连结PE,
则∠DEP为二面角P-BC-A的平面角,
∵PD=2,DE= ,PE=
,PE= ,
,
∴ 。
。
 时,
时,作PD∥AA1
由AA1
当P为A1B的
∵△ABC为正三角形,
∴CD⊥AB,
∴AB⊥平面PCD,
(2)解:过P作PD⊥AB于D,过D作DE⊥BC于E,连结PE,
则∠DEP为二面角P-BC-A的平面角,
∵PD=2,DE=
 ,PE=
,PE= ,
, ∴
 。
。
练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
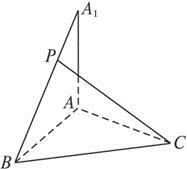 已知AA1⊥平面ABC,AB=BC=AA1=CA,P为A1B上的点.
已知AA1⊥平面ABC,AB=BC=AA1=CA,P为A1B上的点.

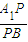 为何值时,AB⊥PC;
为何值时,AB⊥PC;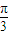 时,求
时,求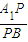 的值.
的值.