题目内容
(本题满分14分)已知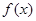 是定义在
是定义在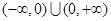 上的奇函数,当
上的奇函数,当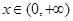 时,
时,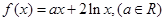
(1)求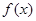 的解析式;
的解析式;
(2)是否存在负实数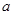 ,使得当
,使得当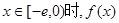 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出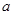 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(3)对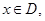 如果函数
如果函数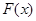 的图像在函数
的图像在函数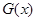 的图像的下方,则称函数
的图像的下方,则称函数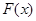 在D上被函数
在D上被函数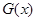 覆盖.求证:若
覆盖.求证:若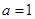 时,函数
时,函数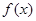 在区间
在区间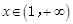 上被函数
上被函数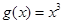 覆盖.
覆盖.
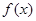 是定义在
是定义在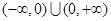 上的奇函数,当
上的奇函数,当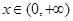 时,
时,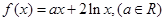
(1)求
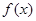 的解析式;
的解析式;(2)是否存在负实数
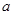 ,使得当
,使得当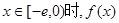 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出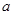 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.(3)对
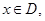 如果函数
如果函数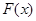 的图像在函数
的图像在函数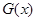 的图像的下方,则称函数
的图像的下方,则称函数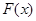 在D上被函数
在D上被函数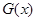 覆盖.求证:若
覆盖.求证:若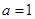 时,函数
时,函数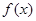 在区间
在区间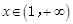 上被函数
上被函数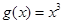 覆盖.
覆盖.(1)
(2)综上知,存在a=-2e满足题意;(3)见解析。

(2)综上知,存在a=-2e满足题意;(3)见解析。
(1)设x∈[-e,0),利用函数为奇函数,得到f(-x)=-f(x),将f(-x)的值代入,求出f(x)在x∈[-e,0)的解析式.
(2)求出f′(x)=0的根,讨论根不在定义域内时,函数在定义域上递增,求出最小值,令最小值等于4,求a;根在定义域内,列出x,f′(x),f(x)d的变化情况表,求出函数的最小值,列出方程求a值.
(3)本小题证明的实质是证明当 时,
时, 恒成立,然后构造函数
恒成立,然后构造函数
 ,利用导数求h(x)的最小值,证明其最小值大于零即可.
,利用导数求h(x)的最小值,证明其最小值大于零即可.



(2)求出f′(x)=0的根,讨论根不在定义域内时,函数在定义域上递增,求出最小值,令最小值等于4,求a;根在定义域内,列出x,f′(x),f(x)d的变化情况表,求出函数的最小值,列出方程求a值.
(3)本小题证明的实质是证明当
 时,
时, 恒成立,然后构造函数
恒成立,然后构造函数 ,利用导数求h(x)的最小值,证明其最小值大于零即可.
,利用导数求h(x)的最小值,证明其最小值大于零即可.



练习册系列答案
相关题目
 (a∈R).
(a∈R).
 ,且
,且 ,则函数
,则函数 ( )
( ) 且
且 是定义在
是定义在 上的偶函数,
上的偶函数, 为奇函数,
为奇函数, ,当
,当 时,
时, ,则在
,则在 内满足方程
内满足方程 的实数
的实数 为
为








 、
、 都是定义在R上的奇函数,且
都是定义在R上的奇函数,且 ,若
,若 ,则
,则




 为奇函数,则
为奇函数,则




 ,若
,若 ,则
,则 _______
_______