题目内容
若F1、F2分别是椭圆
+
=1(a>b>0)的左右焦点,P是该椭圆上的一个动点,且|PF1|+|PF2|=4,|F1F2|=2
.
(1)求出这个椭圆的方程;
(2)是否存在过定点N(0,2)的直线l与椭圆交于不同两点A、B,使∠AOB=90°(其中0为坐标原点)?若存在,求出直线l的斜率k,若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(1)求出这个椭圆的方程;
(2)是否存在过定点N(0,2)的直线l与椭圆交于不同两点A、B,使∠AOB=90°(其中0为坐标原点)?若存在,求出直线l的斜率k,若不存在,请说明理由.
分析:(1)由题设知2a=4,2c=2
,由此能求出椭圆方程.
(2)设l为y=kx+2,A(x1,y1),B(x2,y2),则
⇒(1+4k2)x2+16kx+12=0,故△=(16k)2-4(1+4k2)×12=16(4k2-3)>0⇒k2>
,x1+x2=-
,x1x2=
,由∠AOB=90°,知
•
=0,由此能求出求出直线l的斜率k.
| 3 |
(2)设l为y=kx+2,A(x1,y1),B(x2,y2),则
|
| 3 |
| 4 |
| 16k |
| 1+4k2 |
| 12 |
| 1+4k2 |
| OA |
| OB |
解答:解:(1)∵F1、F2分别是椭圆
+
=1(a>b>0)的左右焦点,
P是该椭圆上的一个动点,且|PF1|+|PF2|=4,|F1F2|=2
,
∴2a=4,2c=2
,
即a=2,c=
,∴b=
=1,
∴椭圆方程为
+y2=1.
(2)当l的斜率不存在时,即x=0不满足题设条件…3
设l为y=kx+2,A(x1,y1),B(x2,y2),
则
⇒(1+4k2)x2+16kx+12=0,
∴△=(16k)2-4(1+4k2)×12=16(4k2-3)>0⇒k2>
,
∴x1+x2=-
,x1x2=
,
∵∠AOB=90°,∴
•
=0,
∴k2=4,k=±2.
| x2 |
| a2 |
| y2 |
| b2 |
P是该椭圆上的一个动点,且|PF1|+|PF2|=4,|F1F2|=2
| 3 |
∴2a=4,2c=2
| 3 |
即a=2,c=
| 3 |
| 4-3 |
∴椭圆方程为
| x2 |
| 4 |
(2)当l的斜率不存在时,即x=0不满足题设条件…3
设l为y=kx+2,A(x1,y1),B(x2,y2),
则
|
∴△=(16k)2-4(1+4k2)×12=16(4k2-3)>0⇒k2>
| 3 |
| 4 |
∴x1+x2=-
| 16k |
| 1+4k2 |
| 12 |
| 1+4k2 |
∵∠AOB=90°,∴
| OA |
| OB |
|
∴k2=4,k=±2.
点评:本题考查椭圆方程的求法,探索直线的斜率是否存在,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
 在左、右焦点,P是该椭圆上的一个动点,且
在左、右焦点,P是该椭圆上的一个动点,且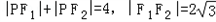 .
.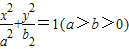 的左右焦点,P是该椭圆上的一个动点,且
的左右焦点,P是该椭圆上的一个动点,且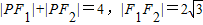 .
. 在左、右焦点,P是该椭圆上的一个动点,且
在左、右焦点,P是该椭圆上的一个动点,且 .
.