题目内容
若F1、F2分别是椭圆
在左、右焦点，P是该椭圆上的一个动点，且
．
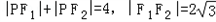（1）求出这个椭圆的方程；
（2）是否存在过定点N（0，2）的直线l与椭圆交于不同的两点A、B，使∠AOB=90°（其中O为坐标原点）？若存在，求出直线l的斜率k，若不存在，请说明理由．
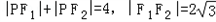在左、右焦点，P是该椭圆上的一个动点，且．（1）求出这个椭圆的方程；
（2）是否存在过定点N（0，2）的直线l与椭圆交于不同的两点A、B，使∠AOB=90°（其中O为坐标原点）？若存在，求出直线l的斜率k，若不存在，请说明理由．
解：（1）依题意，∵
∴2a=4，2c=2
，
∴a=2，c=
，∴
∴椭圆的方程为
；
（2）显然当直线的斜率不存在时，不满足题设条件，
设方程为y=kx+2，A（x1，y1），B（x2，y2）
联立方程组
，
消元可得（1+4k2）x2+16kx+12=0
∴x1+x2=
，
由△=256k2﹣4（1+4k2）×12＞0，
可得
①
∵∠AOB=90°，∴
∴
∴k2=4 ②
①②可得，k=±2
∴2a=4，2c=2
，∴a=2，c=
，∴∴椭圆的方程为
；（2）显然当直线的斜率不存在时，不满足题设条件，
设方程为y=kx+2，A（x1，y1），B（x2，y2）
联立方程组
，消元可得（1+4k2）x2+16kx+12=0
∴x1+x2=
，由△=256k2﹣4（1+4k2）×12＞0，
可得
①∵∠AOB=90°，∴
∴
∴k2=4 ②
①②可得，k=±2
练习册系列答案
相关题目
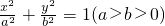在左、右焦点，P是该椭圆上的一个动点，且|PF1|＋|PF2|＝4，|F1F2|＝2
．
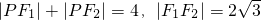在左、右焦点，P是该椭圆上的一个动点，且
．
在左、右焦点，P是该椭圆上的一个动点，且
．