题目内容
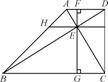
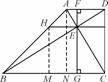
如图，在△ABC中，∠C＝90°，BE是角平分线，DE⊥BE交AB于D，圆O是△BDE的外接圆．
(1) 求证：AC是圆O的切线；
(2) 如果AD＝6，AE＝6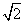
，求BC的长．
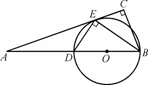
(1) 证明：连OE，∵BE⊥DE，
∴O点为BD的中点．
∵OB＝OE，∴∠OEB＝∠OBE.
∵∠OEC＝∠OEB＋∠CEB＝∠OBE＋∠CEB＝∠CEB＋∠CBE＝90°，即OE⊥AC.
又E是AC与圆O的公共点，∴AC是圆O的切线．
(2) 解：∵AE是圆的切线，∴∠AED＝∠ABE.
又∠A共用，∴△ADE∽△AEB，
∴
解得AB＝12，
∴圆O的半径为3.
又∵OE∥BC，∴
解得BC＝4.
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
.
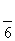