题目内容
已知抛物线 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线 :
: 的左焦点
的左焦点 且垂直于
且垂直于 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线 与双曲线
与双曲线 的一个交点是
的一个交点是 .
.
(1)求抛物线 的方程及其焦点
的方程及其焦点 的坐标;
的坐标;
(2)求双曲线 的方程及其离心率
的方程及其离心率 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由题意可设抛物线 的方程为
的方程为 .
.
把 代入方程
代入方程 ,得
,得
因此,抛物线 的方程为
的方程为 .
.
于是焦点
(2)抛物线 的准线方程为
的准线方程为 ,
,
所以,
而双曲线 的另一个焦点为
的另一个焦点为 ,于是
,于是 
因此,
又因为 ,所以
,所以 .
.
于是,双曲线 的方程 为
的方程 为
因此,双曲线 的离心率
的离心率 .
.
考点:本题主要考查抛物线的标准方程、几何性质,双曲线的定义、标准方程及几何性质。
点评:基础题,围绕的定义、标准方程及几何性质而命制的题目较为常见,a,b,c,e的关系要清楚。

练习册系列答案
相关题目
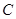 的顶点为坐标原点
的顶点为坐标原点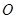 ,焦点
,焦点 在
在 轴上,准线
轴上,准线 与圆
与圆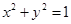 相切.
相切.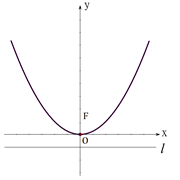
 在抛物线
在抛物线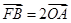 ,求点
,求点 的坐标.
的坐标.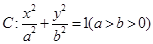 的焦点为
的焦点为 、
、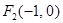 ,离心率为
,离心率为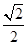 ,过点
,过点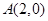 的直线
的直线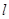 交椭圆
交椭圆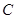 于
于 、
、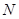 两点.
两点.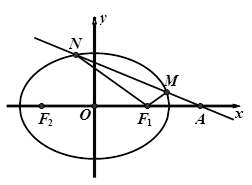
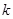 的取值范围;
的取值范围;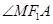 和
和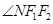 是否总相等?若相等,请给出证明,若不相等,说明理由.
是否总相等?若相等,请给出证明,若不相等,说明理由. 是椭圆
是椭圆 的右顶点,若点
的右顶点,若点 在椭圆上,且满足
在椭圆上,且满足 .(其中
.(其中 为坐标原点)
为坐标原点)
 与椭圆交于两点
与椭圆交于两点 ,当
,当 时,求
时,求 面积的最大值.
面积的最大值.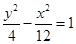 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为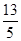 ,若椭圆的焦点在
,若椭圆的焦点在 轴上,求椭圆的方程.
轴上,求椭圆的方程.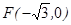 ,且过
,且过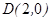 ,设点
,设点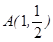 .
.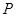 是椭圆上的动点,求线段
是椭圆上的动点,求线段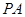 中点
中点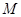 的轨迹方程。
的轨迹方程。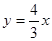 ,右焦点
,右焦点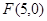 ,双曲线的实轴为
,双曲线的实轴为 ,
,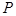 为双曲线上一点(不同于
为双曲线上一点(不同于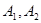 ),直线
),直线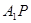 ,
,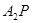 分别与直线
分别与直线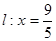 交于
交于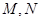 两点
两点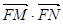 是否为定值,若为定值,求出该值;若不为定值,说明理由。
是否为定值,若为定值,求出该值;若不为定值,说明理由。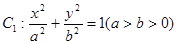 经过点
经过点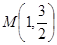 ,且其右焦点与抛物线
,且其右焦点与抛物线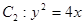 的焦点F重合.
的焦点F重合. 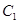 的方程;
的方程;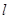 经过点
经过点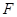 与椭圆
与椭圆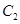 相交于C、D两点.求
相交于C、D两点.求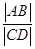 的最大值.
的最大值.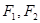 分别是椭圆的
分别是椭圆的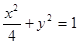 左,右焦点。
左,右焦点。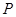 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且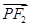 ·
·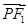 =
=
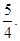 求点
求点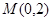 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点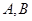 ,且
,且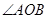 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线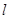 的斜率
的斜率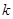 的取值范围。
的取值范围。