题目内容
如图,已知点 是椭圆
是椭圆 的右顶点,若点
的右顶点,若点 在椭圆上,且满足
在椭圆上,且满足 .(其中
.(其中 为坐标原点)
为坐标原点)
(1)求椭圆的方程;
(2)若直线 与椭圆交于两点
与椭圆交于两点 ,当
,当 时,求
时,求 面积的最大值.
面积的最大值.
(1) ;(2)
;(2) 。
。
解析试题分析:(1)因为点 在椭圆上,所以
在椭圆上,所以 ……2分
……2分
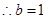 ……4分
……4分 ……5分
……5分
(Ⅱ)设 ,
, ……6分
……6分 ……8分
……8分
设直线 ,由
,由 ,得:
,得:
则
 ……10分
……10分
点 到直线
到直线 的距离
的距离
 ……13分
……13分
当且仅当
所以当 时,
时, 面积的最大值为
面积的最大值为 . ……14分
. ……14分
考点:本题考查了椭圆方程的求法及直线与椭圆的位置关系。
点评:新课标高考对双曲线和抛物线要求较低,重点是椭圆,但也不断加强对圆的考查,所以学习中我们要多做一些与椭圆、圆有关的问题,多记忆一些椭圆、圆的性质.

练习册系列答案
相关题目
 的离心率为
的离心率为 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为 .
. 的方程;
的方程; 与椭圆
与椭圆 两点,坐标原点
两点,坐标原点 到直线
到直线 ,求
,求
 。
。  +
+ =1(a>b>0)的一个焦点是F(1,0),且离心率为
=1(a>b>0)的一个焦点是F(1,0),且离心率为 .
. (
( )所表示的曲线类型.
)所表示的曲线类型. 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
 与抛物线C交于两点
与抛物线C交于两点 ,
, ,且
,且 (a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到
(a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到 .
. 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线 :
: 的左焦点
的左焦点 且垂直于
且垂直于 .
. 的坐标;
的坐标; .
. 、
、 两个岛屿,
两个岛屿,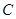 ,曾有渔船在距
,曾有渔船在距 轴,
轴,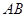 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。
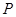 处反射信号的时间比为
处反射信号的时间比为 ,问你能否确定
,问你能否确定 与直线
与直线 交于
交于 两点.
两点. 的长度;
的长度; 在抛物线
在抛物线 上,且
上,且 的面积为
的面积为 ,求点P的坐标.
,求点P的坐标.