题目内容
已知 分别是双曲线
分别是双曲线
 的左、右焦点,若
的左、右焦点,若 关于渐近线的对称点恰落在以
关于渐近线的对称点恰落在以 为圆心,
为圆心, 为半径的圆上,则
为半径的圆上,则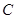 的离心率为( )
的离心率为( )
A. | B. | C.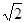 | D. |
D
解析试题分析:设 关于渐近线的对称点为A(x,y),则
关于渐近线的对称点为A(x,y),则 ,另外,双曲线的渐近线为
,另外,双曲线的渐近线为 ,其斜率
,其斜率 ,又求得线段
,又求得线段 的中点
的中点 ,且
,且 ,则有
,则有 ,解得
,解得 ,由
,由 得:
得: ,则
,则 ,将x和y代入
,将x和y代入 得:
得: ,化为
,化为 ,又因为
,又因为 ,所以
,所以 ,解得
,解得 。故选D。
。故选D。
考点:双曲线的性质
点评:求曲线的性质是必考点,做这类题目需结合图形才能较好的解决问题,因而画图是前提。

练习册系列答案
相关题目
若抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知动点 在椭圆
在椭圆 上,若
上,若 点坐标为
点坐标为 ,
, ,且
,且 ,则
,则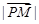 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
直线 与曲线
与曲线 的交点个数为( )
的交点个数为( )
| A.4个 | B.1个 | C.2个 | D.3个 |
如图, 是平面
是平面 的斜线段,
的斜线段, 为斜足。若点
为斜足。若点 在平面
在平面 内运动,使得
内运动,使得 的面积为定值,则动点
的面积为定值,则动点 的轨迹是( )
的轨迹是( )
| A.圆 | B.椭圆 |
| C.一条直线 | D.两条平行直线 |
 和双曲线
和双曲线 有相同的焦点F1、F2,以线段F1F2为边作正△F1F2M,若椭圆与双曲线的一个交点P恰好是MF1的中点,设椭圆和双曲线的离心率分别为
有相同的焦点F1、F2,以线段F1F2为边作正△F1F2M,若椭圆与双曲线的一个交点P恰好是MF1的中点,设椭圆和双曲线的离心率分别为 等于
等于 为抛物线
为抛物线 上一个动点,直线
上一个动点,直线 :
: ,
, :
: ,则
,则



 的左焦点
的左焦点 ,作圆:
,作圆: 的切线,切点为E,延长FE交双曲线右支于点P,若
的切线,切点为E,延长FE交双曲线右支于点P,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )



 的双曲线与圆
的双曲线与圆 的一个交点,则
的一个交点,则 = ( )
= ( )


