题目内容
(本小题满分14分)
动点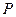 与点
与点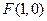 的距离和它到直线
的距离和它到直线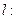
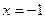 的距离相等,记点
的距离相等,记点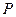 的轨迹为曲线
的轨迹为曲线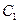 .圆
.圆
的圆心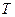 是曲线
是曲线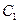 上的动点, 圆
上的动点, 圆 与
与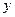 轴交于
轴交于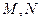 两点,且
两点,且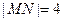 .
.
(1)求曲线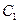 的方程;
的方程;
(2)设点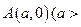 2
2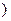 ,若点
,若点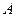 到点
到点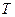 的最短距离为
的最短距离为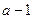 ,试判断直线
,试判断直线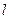 与圆
与圆 的位置关系,
的位置关系,
并说明理由.
动点
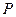 与点
与点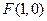 的距离和它到直线
的距离和它到直线
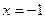 的距离相等,记点
的距离相等,记点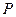 的轨迹为曲线
的轨迹为曲线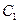 .圆
.圆
的圆心
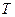 是曲线
是曲线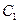 上的动点, 圆
上的动点, 圆 与
与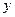 轴交于
轴交于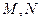 两点,且
两点,且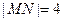 .
.(1)求曲线
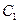 的方程;
的方程;(2)设点
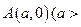 2
2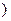 ,若点
,若点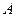 到点
到点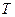 的最短距离为
的最短距离为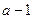 ,试判断直线
,试判断直线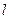 与圆
与圆 的位置关系,
的位置关系,并说明理由.
(本小题满分14分)
(本小题主要考查求曲线的轨迹方程、直线、圆、抛物线等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力、运算求解能力和创新意识)
(1)解法1: 设动点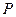 的坐标为
的坐标为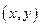 ,依题意,得
,依题意,得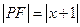 ,
,
即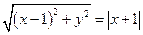 , …… 2分
, …… 2分
化简得: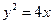 ,
,
∴曲线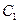 的方程为
的方程为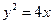 . …… 4分
. …… 4分
解法2:由于动点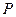 与点
与点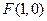 的距离和它到直线
的距离和它到直线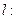
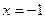 的距离相等,
的距离相等,
根据抛物线的定义可知,动点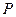 的轨迹是以点
的轨迹是以点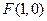 为焦点,直线
为焦点,直线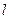 为准线的抛物线.
为准线的抛物线.
…… 2分
∴曲线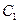 的方程为
的方程为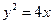 . …… 4分
. …… 4分
(2)解: 设点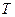 的坐标为
的坐标为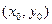 ,圆
,圆 的半径为
的半径为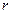 ,
,
∵ 点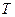 是抛物线
是抛物线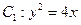 上的动点,
上的动点,
∴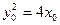 (
(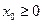 ).
).
∴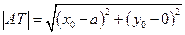 …… 6分
…… 6分
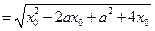
 .
.
∵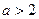 ,∴
,∴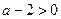 ,则当
,则当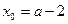 时,
时,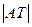 取得最小值为
取得最小值为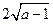 , …… 8分
, …… 8分
依题意得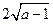
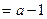 ,
,
两边平方得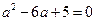 ,
,
解得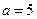 或
或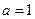 (不合题意,舍去). …… 10分
(不合题意,舍去). …… 10分
∴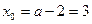 ,
,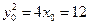 ,即
,即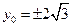 .
.
∴圆 的圆心
的圆心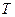 的坐标为
的坐标为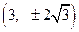 .
.
∵ 圆 与
与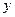 轴交于
轴交于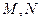 两点,且
两点,且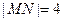 ,
,
∴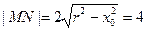 .
.
∴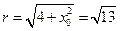 . …… 12分
. …… 12分
∵点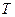 到直线
到直线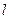 的距离
的距离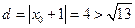 ,
,
∴直线 与圆
与圆 相离. …… 14分
相离. …… 14分
(本小题主要考查求曲线的轨迹方程、直线、圆、抛物线等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力、运算求解能力和创新意识)
(1)解法1: 设动点
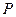 的坐标为
的坐标为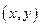 ,依题意,得
,依题意,得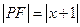 ,
,即
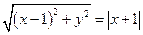 , …… 2分
, …… 2分化简得:
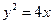 ,
,∴曲线
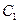 的方程为
的方程为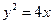 . …… 4分
. …… 4分解法2:由于动点
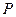 与点
与点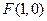 的距离和它到直线
的距离和它到直线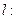
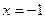 的距离相等,
的距离相等,根据抛物线的定义可知,动点
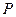 的轨迹是以点
的轨迹是以点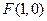 为焦点,直线
为焦点,直线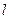 为准线的抛物线.
为准线的抛物线.…… 2分
∴曲线
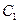 的方程为
的方程为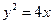 . …… 4分
. …… 4分(2)解: 设点
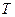 的坐标为
的坐标为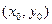 ,圆
,圆 的半径为
的半径为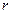 ,
, ∵ 点
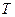 是抛物线
是抛物线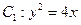 上的动点,
上的动点,∴
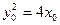 (
(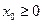 ).
).∴
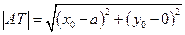 …… 6分
…… 6分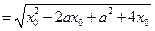
 .
. ∵
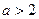 ,∴
,∴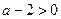 ,则当
,则当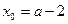 时,
时,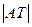 取得最小值为
取得最小值为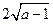 , …… 8分
, …… 8分依题意得
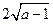
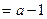 ,
, 两边平方得
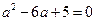 ,
,解得
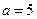 或
或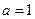 (不合题意,舍去). …… 10分
(不合题意,舍去). …… 10分∴
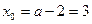 ,
,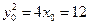 ,即
,即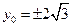 .
.∴圆
 的圆心
的圆心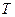 的坐标为
的坐标为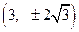 .
.∵ 圆
 与
与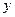 轴交于
轴交于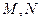 两点,且
两点,且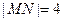 ,
,∴
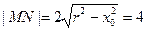 .
.∴
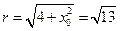 . …… 12分
. …… 12分∵点
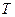 到直线
到直线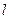 的距离
的距离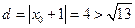 ,
,∴直线
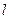 与圆
与圆 相离. …… 14分
相离. …… 14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
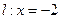 ,
,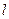 与
与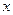 轴交于点
轴交于点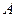 ,动点
,动点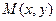 到直线
到直线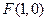 的距离大
的距离大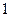 .
.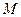 的轨迹
的轨迹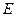
 的方程;
的方程; 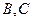 两点,若
两点,若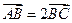 ,求此直线的方程.
,求此直线的方程.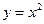 ,
,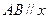 轴.
轴.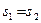 时,求P点的坐标。
时,求P点的坐标。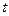 的值,使
的值,使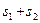 的值最小,并求出最小值。
的值最小,并求出最小值。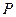 (4,
(4,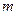 )到焦点的距离为5.
)到焦点的距离为5.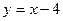 相交于不同的两点A、B,求证:
相交于不同的两点A、B,求证:
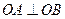 .
.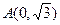 、
、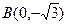 的距离之和为4.
的距离之和为4.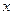 轴的垂线段PD,D为垂足,当P在曲线C上运动时,线段PD的中点M的轨迹是什么?
轴的垂线段PD,D为垂足,当P在曲线C上运动时,线段PD的中点M的轨迹是什么?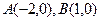 的距离之比等于2的点的轨迹方程。
的距离之比等于2的点的轨迹方程。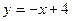 与曲线
与曲线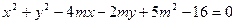 相交于
相交于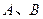 两点,若
两点,若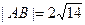 ,求
,求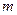 的值.
的值.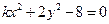 所表示的曲线.
所表示的曲线.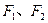 为椭圆
为椭圆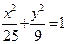 的两个焦点,过
的两个焦点,过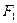 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若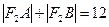 ,则
,则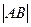 =_______.
=_______.