题目内容
不等式ax2+5x+c＜0的解集是{x|x＞6，或x＜-1}，则cx2+5x+a＜0的解集是________．
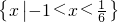
分析：由不等式ax2+5x+c＜0的解集是{x|x＞6，或x＜-1}可知，a＜0，且满足6-1=
，且6×（-1）=
，可解得a=-1，c=6．所以不等式cx2+5x+a＜0可化为6x2+5x-1＜0，解之即可得到答案．解答：由不等式ax2+5x+c＜0的解集是{x|x＞6，或x＜-1}可知：a＜0，
且方程ax2+5x+c=0的两实根为：-1，6，由根与系数可得，
6-1=
，且6×（-1）=，可解得a=-1，c=6．所以不等式cx2+5x+a＜0即6x2+5x-1＜0
由于方程6x2+5x-1=0的两根为-1，
，故不等式的解集为：{
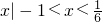}，故答案为：{
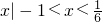}．点评：本题为一元二次不等式的解法，用好一元二次方程与一元二次不等式的关系是解决问题的关键，属基础题．
练习册系列答案
相关题目