题目内容
设a>0且a≠1,函数f(x)=a
有最大值,则不等式ax2-5x+6>1的解集为 .
| x2-2x+3 |
分析:根据函数f(x)=a
有最大值,可得0<a<1,故由不等式ax2-5x+6>1=a0 可得 x2-5x+6<0,由此求得不等式的解集.
| x2-2x+3 |
解答:解:∵函数f(x)=a
有最大值,
∴0<a<1,
不等式ax2-5x+6>1=a0
∴x2-5x+6<0,解得2<x<3,
故答案为:{x|2<x<3}.
| x2-2x+3 |
∴0<a<1,
不等式ax2-5x+6>1=a0
∴x2-5x+6<0,解得2<x<3,
故答案为:{x|2<x<3}.
点评:本题主要考查指数函数的图象和性质,指数不等式的解法,属于中档题.

练习册系列答案
相关题目
 的定义域为D,若对于任意
的定义域为D,若对于任意
 ,当
,当 时,都有
时,都有 ,则称函
,则称函 ; ②
; ② ; ③
; ③ .
. 等于( )
等于( ) B.
B. C.
C. D.无法确定
D.无法确定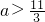 ;
;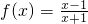 ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.