题目内容
如图，四棱锥P-ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M是AC的中点，点N在线段PB上，且∠CAD=30°，PA=AB=4．（Ⅰ）当MN∥平面PDC时，求
| PN |
| NB |
（Ⅱ）当N为PB的中点时，求二面角N-AC-P的余弦值．
考点：与二面角有关的立体几何综合题,直线与平面平行的性质
专题：空间位置关系与距离,空间角
分析：（Ⅰ）当MN∥平面PDC时，由线面平行的性质定理可得MN∥PD，进而PN：NB=DM：MB，结合已知可得
的值；
（Ⅱ）以A为原点，直线AB，AD，AP为x，y，z轴建立空间直角坐标系，求出当N为PB的中点时，平面AMN的一个法向量和平面ACP的一个法向量，代入向量公式可得二面角N-AC-P的余弦值．
| PN |
| NB |
（Ⅱ）以A为原点，直线AB，AD，AP为x，y，z轴建立空间直角坐标系，求出当N为PB的中点时，平面AMN的一个法向量和平面ACP的一个法向量，代入向量公式可得二面角N-AC-P的余弦值．
解答：
解：（Ⅰ）∵MN∥平面PDC，MN?平面PBD，
平面PBD∩平面PDC=PD，
∴MN∥PD，
∴PN：NB=DM：MB，
在等边△ABC中，M为AC的中点，PA=AB=4
∴BM=2
，AM=2，BM⊥AC，
∵∠CAD=30°，
∴DM=
，
∴DM：MB=1：3，
即
=
，
（II）∵∠BAC=60°，∠CAD=30°，
∴∠BAD=90°，即BA⊥AD，
又由PA⊥平面ABCD，
∴PA⊥AB，PA⊥AC，
以A为原点，直线AB，AD，AP为x，y，z轴建立空间直角坐标系，
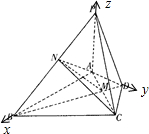
则P（0，0，4），B（4，0，0），N（2，0，2），
∴
=（2，0，2），
过M作ME垂直AB于点E，MF垂直AD于点F，则ME=
，MF=1，
∴M（1，
，0），
∴
=（1，
，0），
设平面AMN的一个法向量
=（x，y，z），
则
，令x=3，则
=（3，-
，-3），
又∵PA⊥平面ABCD，
∴PA⊥BM，
∵BM⊥AC，AC，PA?平面ACP，AC∩PA=A，
∴BM⊥平面ACP，
=（3，-
，0）为平面ACP的一个法向量，
设二面角N-AC-P的平面角为θ，
则cosθ=
=
=
即二面角N-AC-P的余弦值为：
平面PBD∩平面PDC=PD，
∴MN∥PD，
∴PN：NB=DM：MB，
在等边△ABC中，M为AC的中点，PA=AB=4
∴BM=2
| 3 |
∵∠CAD=30°，
∴DM=
2
| ||
| 3 |
∴DM：MB=1：3，
即
| PN |
| NB |
| 1 |
| 3 |
（II）∵∠BAC=60°，∠CAD=30°，
∴∠BAD=90°，即BA⊥AD，
又由PA⊥平面ABCD，
∴PA⊥AB，PA⊥AC，
以A为原点，直线AB，AD，AP为x，y，z轴建立空间直角坐标系，
则P（0，0，4），B（4，0，0），N（2，0，2），
∴
| AN |
过M作ME垂直AB于点E，MF垂直AD于点F，则ME=
| 3 |
∴M（1，
| 3 |
∴
| AM |
| 3 |
设平面AMN的一个法向量
. |
| m |
则
|
. |
| m |
| 3 |
又∵PA⊥平面ABCD，
∴PA⊥BM，
∵BM⊥AC，AC，PA?平面ACP，AC∩PA=A，
∴BM⊥平面ACP，
| MB |
| 3 |
设二面角N-AC-P的平面角为θ，
则cosθ=
|
| ||||
|
|
| 12 | ||||
|
2
| ||
| 7 |
即二面角N-AC-P的余弦值为：
2
| ||
| 7 |
点评：本题考查的知识点是与二面角有关的立体几何综合体，直线与平面平行的性质，综合性质强，难度中档．
练习册系列答案
名校课堂系列答案
相关题目