题目内容
设二项展开式Cn=(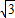 +1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.
+1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.(1)计算C1B1,C2B2的值;
(2)求CnBn.
【答案】分析:(1)将n分别用1,2 代替求出C1,C2,利用多项式的乘法展开,求出C1,C2的小数部分B1,B2,求出C1B1,C2B2的值.
(2)利用二项式定理表示出Cn,再利用二项式定理表示出 ,两个式子相减得到展开式的整数部分和小数部分,求出CnBn的值.
,两个式子相减得到展开式的整数部分和小数部分,求出CnBn的值.
解答:解:(1)因为 ,
,
所以 ,A1=2,
,A1=2, ,所以C1B1=2;
,所以C1B1=2;
又 ,其整数部分A2=20,小数部分
,其整数部分A2=20,小数部分 ,
,
所以C2B2=8.
(2)因为
 ①
①
而 ②
②
①-②得:

 =2(
=2( )
)
而 ,所以
,所以 ,
,
所以 .
.
点评:解决二项式的有关问题一般利用二项式定理;解决二项展开式的通项问题常利用的工具是二项展开式的通项公式.
(2)利用二项式定理表示出Cn,再利用二项式定理表示出
 ,两个式子相减得到展开式的整数部分和小数部分,求出CnBn的值.
,两个式子相减得到展开式的整数部分和小数部分,求出CnBn的值.解答:解:(1)因为
 ,
,所以
 ,A1=2,
,A1=2, ,所以C1B1=2;
,所以C1B1=2;又
 ,其整数部分A2=20,小数部分
,其整数部分A2=20,小数部分 ,
,所以C2B2=8.
(2)因为

 ①
①而
 ②
②①-②得:

 =2(
=2( )
)而
 ,所以
,所以 ,
,
所以
 .
.点评:解决二项式的有关问题一般利用二项式定理;解决二项展开式的通项问题常利用的工具是二项展开式的通项公式.

练习册系列答案
相关题目
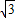 +1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.
+1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.