题目内容
设二项展开式Cn=(
+1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.
(1)计算C1B1,C2B2的值;
(2)求CnBn.
| 3 |
(1)计算C1B1,C2B2的值;
(2)求CnBn.
(1)因为Cn=(
+1)2n-1,
所以C1=
+1,A1=2,B1=
-1,所以C1B1=2;
又C2=(
+ 1)3=10+6
,其整数部分A2=20,小数部分B2=6
-10,
所以C2B2=8.
(2)因为Cn=(
+1)2n-1=
(
)2n-1+
(
)2n-2+…+
+
①
而(
-1)2n-1=
(
)2n-1
(
)2n-2+…+
+
②
①-②得:
(
+1)2n-1 -(
-1)2n-1=2(
(
)2n-2+
(
)2n-4+…+
)
而0<(
-1)2n-1<1,所以An=(
+1)2N-1-(
-1)2n-1,Bn=(
-1)2N-1
所以CnBn=(
+1)2n-1(
-1)2n-1=22n-1.
| 3 |
所以C1=
| 3 |
| 3 |
又C2=(
| 3 |
| 3 |
| 3 |
所以C2B2=8.
(2)因为Cn=(
| 3 |
| C | 02n-1 |
| 3 |
| C | 12n-1 |
| 3 |
| C | 2n-22n-1 |
| 3 |
| C | 2n-12n-1 |
而(
| 3 |
| C | 02n-1 |
| 3 |
| C | 12n-1 |
| 3 |
| C | 2n-22n-1 |
| 3 |
| -C | 2n-12n-1 |
①-②得:
(
| 3 |
| 3 |
| C | 12n-1 |
| 3 |
| C | 32n-1 |
| 3 |
| C | 2n-12n-1 |
而0<(
| 3 |
| 3 |
| 3 |
| 3 |
所以CnBn=(
| 3 |
| 3 |

练习册系列答案
相关题目
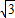 +1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.
+1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.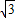 +1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.
+1)2n-1(n∈N*)的整数部分为An,小数部分为Bn.