题目内容
(本题满分![]() 分)
分)
已知函数![]() 和点
和点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() .
.
(Ⅰ)设![]() ,试求函数
,试求函数![]() 的表达式;
的表达式;
(Ⅱ)是否存在![]() ,使得
,使得![]() 、
、![]() 与
与![]() 三点共线.若存在,求出
三点共线.若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数![]() ,在区间
,在区间![]() 内总存在
内总存在![]() 个实数
个实数
![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,求
成立,求![]() 的最大值.
的最大值.
(本小题满分14分)
解:(Ⅰ)设![]() 、
、![]() 两点的横坐标分别为
两点的横坐标分别为![]() 、
、![]() ,
,
![]()
![]() ,
, ![]() 切线
切线![]() 的方程为:
的方程为:![]() ,
,
又![]() 切线
切线![]() 过点
过点![]() ,
, ![]() 有
有![]() ,
,
即![]() , ………………………………………………(1) …… 2分
, ………………………………………………(1) …… 2分
同理,由切线![]() 也过点
也过点![]() ,得
,得![]() .…………(2)
.…………(2)
由(1)、(2),可得![]() 是方程
是方程![]() 的两根,
的两根,
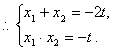 ………………( * ) ……………………… 4分
………………( * ) ……………………… 4分

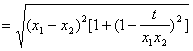
 ,
,
把( * )式代入,得![]() ,
,
因此,函数![]() 的表达式为
的表达式为![]() . ……………………5分
. ……………………5分
(Ⅱ)当点![]() 、
、![]() 与
与![]() 共线时,
共线时,![]() ,
,![]()
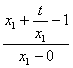 =
=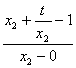 ,
,
即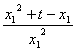 =
=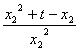 ,化简,得
,化简,得![]() ,
,
,![]() . ………………(3) …………… 7分
. ………………(3) …………… 7分
把(*)式代入(3),解得![]() .
.
![]() 存在
存在![]() ,使得点
,使得点![]() 、
、![]() 与
与![]() 三点共线,且
三点共线,且 ![]() . ……………………9分
. ……………………9分
(Ⅲ)解法![]() :易知
:易知![]() 在区间
在区间![]() 上为增函数,
上为增函数,
![]()
![]()
![]() ,
,
则![]() .
.
依题意,不等式![]() 对一切的正整数
对一切的正整数![]() 恒成立, …………11分
恒成立, …………11分
![]() ,
,
即![]() 对一切的正整数
对一切的正整数![]() 恒成立,.
恒成立,.
![]() ,
, ![]() ,
,
![]() .
.
由于![]() 为正整数,
为正整数,![]() . ……………………………13分
. ……………………………13分
又当![]() 时,存在
时,存在![]() ,
,![]() ,对所有的
,对所有的![]() 满足条件.
满足条件.
因此,![]() 的最大值为
的最大值为![]() . ……………………………14分
. ……………………………14分
解法![]() :依题意,当区间
:依题意,当区间![]() 的长度最小时,得到的
的长度最小时,得到的![]() 最大值,即是所求值.
最大值,即是所求值.
![]() ,
,![]() 长度最小的区间为
长度最小的区间为![]() , …………………11分
, …………………11分
当![]()
![]() 时,与解法
时,与解法![]() 相同分析,得
相同分析,得![]() ,
,
解得![]() . ……………………………13分
. ……………………………13分
后面解题步骤与解法![]() 相同(略).
相同(略).

 的值.
的值.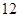 分)已知函数
分)已知函数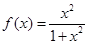 .
.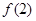 与
与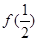 ,
,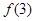 与
与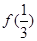 ;
;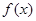 与
与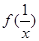 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;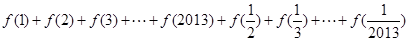 的值 .
的值 .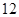 分)已知双曲线
分)已知双曲线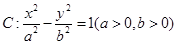 的离心率为
的离心率为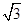 ,且双曲线上点到右焦点的距离与到直线
,且双曲线上点到右焦点的距离与到直线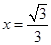 的距离之比为
的距离之比为 的方程;
的方程; 与双曲线
与双曲线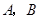 ,且线段
,且线段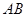 的中点在圆
的中点在圆 上,求
上,求 的值.
的值. 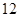 分)已知抛物线的顶点在坐标原点,焦点在
分)已知抛物线的顶点在坐标原点,焦点在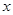 轴正半轴,抛物线上一点
轴正半轴,抛物线上一点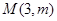 到焦点的距离为
到焦点的距离为 ,求
,求 的值及抛物线方程.
的值及抛物线方程.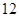 分)已知命题
分)已知命题 :关于
:关于 的一元二次方程
的一元二次方程 有两个不相等的实数根,命题
有两个不相等的实数根,命题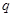 :
:
 是增函数,若
是增函数,若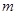 的取值范围.
的取值范围.