题目内容
(1)求证:2n+2•3n+5n-4能被25整除.
(2)求证:
-
+
-
+…+(-1)n•
=
.
(2)求证:
| C | 0 n |
| 1 |
| 2 |
| C | 1 n |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 4 |
| C | 3 n |
| 1 |
| n+1 |
| C | n n |
| 1 |
| n+1 |
分析:(1)用数学归纳法证明:①当n=1时,2n+2•3n+5n-4=8×3+5-4=25,能被25整除;②假设n=k时,2k+2•3k+5k-4能被25整除,由此导出当n=k+1时,2k+3•3k+1+5(k+1)-4能被25整除即可.
(2))由
=
•
=
,能够证明
-
+
-
+…+(-1)n•
=
.
(2))由
| 1 |
| r+1 |
| C | r n |
| 1 |
| r+1 |
| n! |
| r!(n-r)! |
| 1 |
| n+1 |
| C | r+1 n+1 |
| C | 0 n |
| 1 |
| 2 |
| C | 1 n |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 4 |
| C | 3 n |
| 1 |
| n+1 |
| C | n n |
| 1 |
| n+1 |
解答:证明:(1)用数学归纳法证明:
①当n=1时,2n+2•3n+5n-4=8×3+5-4=25,能被25整除,成立;
②假设n=k时,成立,即2k+2•3k+5k-4能被25整除,
则当n=k+1时,2k+3•3k+1+5(k+1)-4=6(2k+2•3k)+5k+5-4
=(2k+2•3k+5k-4)+5(2k+2•3k)+5
=(2k+2•3k+5k-4)+20•6k+5,
∵2k+2•3k+5k-4能被5整除,20•6k+5能被25整除,
∴(2k+2•3k+5k-4)+20•6k+5能被25整除,即n=k+1时成立.
由①②知2n+2•3n+5n-4能被25整除.
(2)∵
=
•
=
×
=
,
∴
-
+
-
+…+(-1)n•
=
[
-
+
+…+(-1)nC
],
当n为奇数时,
-
+
+…+(-1)nC
=(
+
+…+
)-(
+
+…+
)
=
=1.
当n为偶数时,
-
+
+…+(-1)nC
=(
+
+…+
)+(
+
+…+C
=
=1.
∴
[
-
+
+…+(-1)nC
]=
.
∴
-
+
-
+…+(-1)n•
=
.
①当n=1时,2n+2•3n+5n-4=8×3+5-4=25,能被25整除,成立;
②假设n=k时,成立,即2k+2•3k+5k-4能被25整除,
则当n=k+1时,2k+3•3k+1+5(k+1)-4=6(2k+2•3k)+5k+5-4
=(2k+2•3k+5k-4)+5(2k+2•3k)+5
=(2k+2•3k+5k-4)+20•6k+5,
∵2k+2•3k+5k-4能被5整除,20•6k+5能被25整除,
∴(2k+2•3k+5k-4)+20•6k+5能被25整除,即n=k+1时成立.
由①②知2n+2•3n+5n-4能被25整除.
(2)∵
| 1 |
| r+1 |
| C | r n |
| 1 |
| r+1 |
| n! |
| r!(n-r)! |
| 1 |
| n+1 |
| (n+1)! |
| (r+1)!(n-r)! |
| 1 |
| n+1 |
| C | r+1 n+1 |
∴
| C | 0 n |
| 1 |
| 2 |
| C | 1 n |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 4 |
| C | 3 n |
| 1 |
| n+1 |
| C | n n |
=
| 1 |
| n+1 |
| C | 1 n+1 |
| C | 2 n+1 |
| C | 3 n+1 |
n+1 n+1 |
当n为奇数时,
| C | 1 n+1 |
| C | 2 n+1 |
| C | 3 n+1 |
n+1 n+1 |
=(
| C | 1 n+1 |
| C | 3 n+1 |
| C | n n+1 |
| C | 2 n+1 |
| C | 4 n+1 |
| C | n+1 n+1 |
=
| C | 0 n+1 |
当n为偶数时,
| C | 1 n+1 |
| C | 2 n+1 |
| C | 3 n+1 |
n+1 n+1 |
=(
| C | 1 n+1 |
| C | 3 n+1 |
| C | n+1 n+1 |
| C | 2 n+1 |
| C | 4 n+1 |
| C | n n+1 |
=
| C | 0 n+1 |
∴
| 1 |
| n+1 |
| C | 1 n+1 |
| C | 2 n+1 |
| C | 3 n+1 |
n+1 n+1 |
| 1 |
| n+1 |
∴
| C | 0 n |
| 1 |
| 2 |
| C | 1 n |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 4 |
| C | 3 n |
| 1 |
| n+1 |
| C | n n |
| 1 |
| n+1 |
点评:本题考查数学归纳法的应用,考查二项式定理的应用.解题时要认真审题,仔细分析组合数性质,注意合理地进行等价转化.

练习册系列答案
相关题目
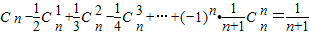 .
.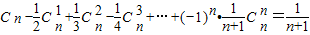 .
.