题目内容
(本小题满分12分)设函数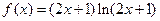 .
.
(Ⅰ)求函数f (x)在点(0, f (0))处的切线方程;
(Ⅱ)求f (x)的极小值;
(Ⅲ)若对所有的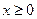 ,都有
,都有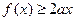 成立,求实数a的取值范围.
成立,求实数a的取值范围.
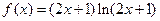 .
.(Ⅰ)求函数f (x)在点(0, f (0))处的切线方程;
(Ⅱ)求f (x)的极小值;
(Ⅲ)若对所有的
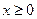 ,都有
,都有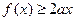 成立,求实数a的取值范围.
成立,求实数a的取值范围.y=2x,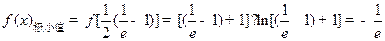
(-∞,1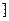 .
.
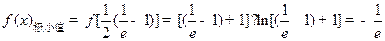
(-∞,1
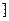 .
.(Ⅰ)∵f(x)的定义域为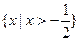 ,又∵
,又∵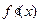 =2ln(2x+1)+2,
=2ln(2x+1)+2,
∴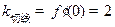 ,切点为O(0,0),∴所求切线方程为y=2x. …………2分
,切点为O(0,0),∴所求切线方程为y=2x. …………2分
(Ⅱ) 设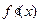 =0,得ln(2x+1)=-1,得
=0,得ln(2x+1)=-1,得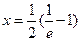 ;
;
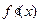 >0,得ln(2x+1)>-1,得
>0,得ln(2x+1)>-1,得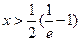 ;
;
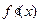 <0,得ln(2x+1)<-1,得
<0,得ln(2x+1)<-1,得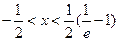 ;
;
则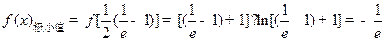 .…………6分
.…………6分
(Ⅲ)令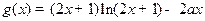 ,
,
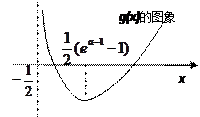 则
则 =2ln(2x+1)+2-2a=2[ln(2x+1)+1-a].
=2ln(2x+1)+2-2a=2[ln(2x+1)+1-a].
令 =0,得ln(2x+1)= a-1,得
=0,得ln(2x+1)= a-1,得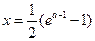 ;
;
 >0,得ln(2x+1)> a-1,得
>0,得ln(2x+1)> a-1,得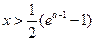 ;
;
 <0,得ln(2x+1)< a-1,得
<0,得ln(2x+1)< a-1,得 ;
;
(1)当a≤1时,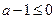 ,∵
,∵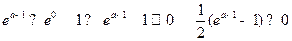 ,
,
∴对所有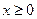 时,都有
时,都有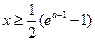 ,于是
,于是 ≥0恒成立,
≥0恒成立,
∴g(x)在[0,+∞)上是增函数.
又g(0)=0,于是对所有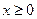 ,都有g(x)≥ g(0)=0成立.
,都有g(x)≥ g(0)=0成立.
故当a≤1时,对所有的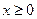 ,都有
,都有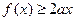 成立.
成立.
(2)当a>1时,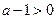 ,∵
,∵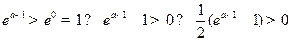 ,
,
∴对所有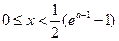 ,都有
,都有 <0恒成立,
<0恒成立,
∴g(x)在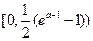 上是减函数.
上是减函数.
又g(0)=0,于是对所有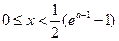 ,都有g(x)≤ g (0)=0.
,都有g(x)≤ g (0)=0.
故当a>1时,只有对仅有的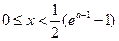 ,都有
,都有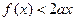 .
.
即当a>1时,不是对所有的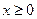 ,都有
,都有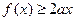 .
.
综合(1),(2)可知实数a的取值范围(-∞,1 .……………………12分
.……………………12分
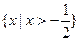 ,又∵
,又∵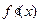 =2ln(2x+1)+2,
=2ln(2x+1)+2,∴
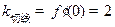 ,切点为O(0,0),∴所求切线方程为y=2x. …………2分
,切点为O(0,0),∴所求切线方程为y=2x. …………2分(Ⅱ) 设
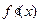 =0,得ln(2x+1)=-1,得
=0,得ln(2x+1)=-1,得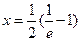 ;
;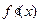 >0,得ln(2x+1)>-1,得
>0,得ln(2x+1)>-1,得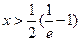 ;
;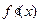 <0,得ln(2x+1)<-1,得
<0,得ln(2x+1)<-1,得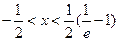 ;
;则
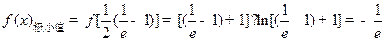 .…………6分
.…………6分(Ⅲ)令
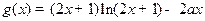 ,
,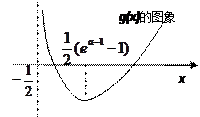 则
则 =2ln(2x+1)+2-2a=2[ln(2x+1)+1-a].
=2ln(2x+1)+2-2a=2[ln(2x+1)+1-a].令
 =0,得ln(2x+1)= a-1,得
=0,得ln(2x+1)= a-1,得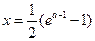 ;
; >0,得ln(2x+1)> a-1,得
>0,得ln(2x+1)> a-1,得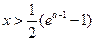 ;
; <0,得ln(2x+1)< a-1,得
<0,得ln(2x+1)< a-1,得 ;
;(1)当a≤1时,
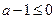 ,∵
,∵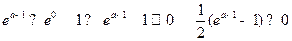 ,
,∴对所有
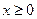 时,都有
时,都有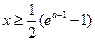 ,于是
,于是 ≥0恒成立,
≥0恒成立,∴g(x)在[0,+∞)上是增函数.
又g(0)=0,于是对所有
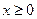 ,都有g(x)≥ g(0)=0成立.
,都有g(x)≥ g(0)=0成立.故当a≤1时,对所有的
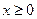 ,都有
,都有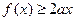 成立.
成立.(2)当a>1时,
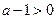 ,∵
,∵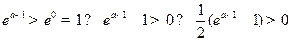 ,
,∴对所有
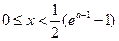 ,都有
,都有 <0恒成立,
<0恒成立,∴g(x)在
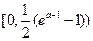 上是减函数.
上是减函数. 又g(0)=0,于是对所有
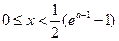 ,都有g(x)≤ g (0)=0.
,都有g(x)≤ g (0)=0.故当a>1时,只有对仅有的
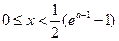 ,都有
,都有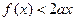 .
.即当a>1时,不是对所有的
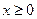 ,都有
,都有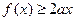 .
.综合(1),(2)可知实数a的取值范围(-∞,1
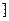 .……………………12分
.……………………12分
练习册系列答案
相关题目
 的导函数为
的导函数为 ,若对任意实数x,都有
,若对任意实数x,都有 ,则
,则 等于 ( )
等于 ( )
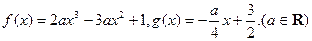
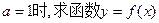 的单调区间;
的单调区间;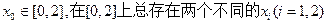 ,使得
,使得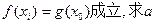 的取值范围.
的取值范围.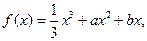 且
且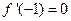
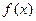 的单调区间;
的单调区间; 

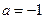 ,设函数
,设函数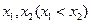 处取得极值
处取得极值 ,记点
,记点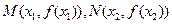 ,证明:线段
,证明:线段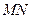 与曲线
与曲线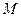 、
、
 的公共点;
的公共点;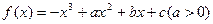 ,在
,在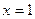 处取得极大值,且存在斜率为
处取得极大值,且存在斜率为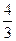 的切线。
的切线。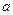 的取值范围;
的取值范围;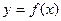 在区间
在区间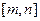 上单调递增,求
上单调递增,求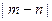 的取值范围;
的取值范围;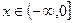 ,都有
,都有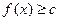 。
。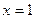 是函数
是函数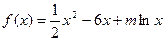 的一个极值点。
的一个极值点。 ;
;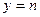 与函数
与函数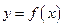 的图象有3个交点,求
的图象有3个交点,求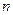 的取值范围;
的取值范围;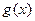 =(
=(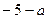 )
)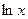 +
+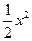 +(6-
+(6-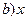 +2(
+2(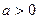 ),
),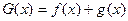 ,若
,若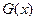 =0有两个零点
=0有两个零点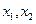 ,且
,且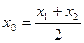 ,试探究
,试探究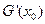 值的符号
值的符号
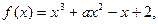
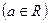
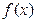 在
在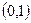 上是减函数,求
上是减函数,求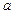 的最大值;
的最大值;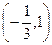 ,求函数y=
,求函数y=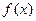 图像过点
图像过点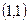 的切线与两坐标轴围成图形的面积。
的切线与两坐标轴围成图形的面积。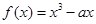 (
(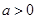 )的零点都在区间[-10,10]上,则使得方程
)的零点都在区间[-10,10]上,则使得方程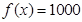 有正整数解的实数
有正整数解的实数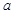 的取值个数为 ( )
的取值个数为 ( )